Abstract
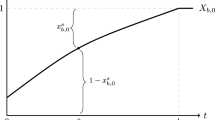
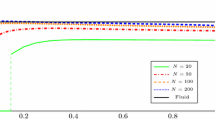
A single-server queueing system with preemptive access is considered. Each customer has one attempt to enter the system at its working interval [0, T]. As soon as the customer request enters the system, the server immediately starts the service. But when the next request arrives in the system, the previous one leaves the system even he has not finished his service yet. We study a non-cooperative game in which the customers wish to maximize their probability of obtaining service within a certain period of time. We characterize the Nash equilibrium and the price of anarchy, which is defined as the ratio between the optimal and equilibrium social utility. Two models are considered. In the first model the number of players is fixed, while in the second it is random and obeys the Poisson distribution. We demonstrate that there exists a unique symmetric equilibrium for both models. Finally, we calculate the price of anarchy for both models and show that the price of anarchy is not monotone with respect to the number of customers.


Similar content being viewed by others
References
Breinbjerg, J., Platz, T.T., Østerdal, L.P.: Equilibrium arrivals to a last-come first-served preemptive-resume queue, Copenhagen Business School, Department of Economics (2020) https://ideas.repec.org/p/hhs/cbsnow/2020_017.html
Teraoka, Y., Hohjo, H.: N-person silent game on sale. Sci. Math. Jpn. 63(2), 237–240 (2006)
Altman, E., Shimkin, N.: Individually optimal dynamic routing in a processor sharing system. Oper. Res. 46, 776–784 (1998)
Chirkova, Yu.V.: Optimal arrivals in a two-server random access system with loss. Autom. Remote Control 78(3), 557–580 (2017)
Dimitriou, I.: A queueing system for modeling cooperative wireless networks with coupled relay nodes and synchronized packet arrivals. Perform. Eval. 114(C), 16–31 (2017)
Mercer, A.: A queueing problem in which the arrival times of the customers are scheduled. J. R. Stat. Soc. Ser. B (Methodological). 108–113 (1960)
Glazer, A., Hassin, R.: ?/M/1: on the equilibrium distribution of customer arrivals. Eur. J. Oper. Res. 13, 146–150 (1983)
Haviv, M.: When to arrive at a queue with tardiness costs. Perform. Eval. 70, 387–399 (2013)
Glazer, A., Hassin, R.: Equilibrium arrivals in queues with bulk service at scheduled times. Transp. Sci. 21, 273–278 (1987)
Mazalov, V.V., Chuiko, J.V.: Nash equilibrium in the optimal arrival time problem. Comput. Technol. 11, 60–71 (2006)
Jain, R., Juneja, S., Shimkin, N.: The concert queueing game: to wait or to be late. Discret. Event Dyn. Syst. 21, 103–138 (2011)
Haviv, M., Ravner, L.: A survey of queueing systems with strategic timing of arrivals. Queueing Syst. 99, 163–198 (2021)
Chirkova, J., Mazalov, V., Morozov, E.: Equilibrium in a queueing system with retrials. Mathematics 10(3), 428 (2022)
Hassin, R., Kleiner, Y.: Equilibrium and optimal arrival patterns to a server with opening and closing times. IIE Trans. 43, 164–175 (2011)
Haviv, M., Kella, O., Kerner, Y.: Equilibrium strategies in queues based on time or index of arrival. Prob. Eng. Inform. Sci. 24, 13–25 (2010)
Ravner, L., Haviv, M.: Equilibrium and socially optimal arrivals to a single server loss system. In: Int. Conf. on Network Games Control and Optimization 2014 (NETGCOOP’14), pp. 119–126, Trento, Italy (2014)
Ravner, L., Haviv, M.: Strategic timing of arrivals to a finite queue multi-server loss system. Queueing Syst. 81, 71–96 (2015)
Mazalov, V., Chirkova, J.: Networking games. Academic Press, Cambridge, MA, USA, Network Forming Games and Games on Networks (2019)
Yamazaki, G.: The GI/G/1 queue with last-come-first-served. Ann. Inst. Stat. Math. 34(3), 599–604 (1982)
Fakinos, D.: The G/G/1 queueing system with a particular queue discipline. J. R. Stat. Soc. Ser. B (Methodological) 43(2), 190–196 (1981)
Chirkova, J., Mazalov, V.: Optimal arrivals to preemptive queueing system. Lect. Notes Comput. Sci. 13367, 169–181 (2022)
Author information
Authors and Affiliations
Contributions
The authors contributed equally to this work. Conceptualization, J. Chirkova, V. Mazalov; methodology, J. Chirkova, V. Mazalov; software, J. Chirkova, V. Mazalov; validation, J. Chirkova, V. Mazalov; formal analysis, J. Chirkova, V. Mazalov; investigation, J. Chirkova, V. Mazalov; resources, J. Chirkova, V. Mazalov; data curation, J. Chirkova, V. Mazalov; writing original draft preparation, J. Chirkova, V. Mazalov; writing review and editing, J. Chirkova, V. Mazalov; visualization, J. Chirkova, V. Mazalov; supervision, J. Chirkova, V. Mazalov. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare no conflict of interest.
Additional information
This research was supported by the Russian Science Foundation (No. 22-11-20015, https://rscf.ru/project/22-11-20015/), jointly with support of the authorities of the Republic of Karelia with funding from the Venture Investment Foundation of the Republic of Karelia. Also the research was supported by the National Natural Science Foundation of China (No. 72171126).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Chirkova, J., Mazalov, V. Equilibrium Arrivals to Preemptive Queueing System with Fixed and Random Population Size. J. Oper. Res. Soc. China 12, 77–92 (2024). https://doi.org/10.1007/s40305-023-00461-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40305-023-00461-9
Keywords
- Service system
- Preemptive priorities
- Strategic users
- Random number of players
- Optimal arrivals
- Kolmogorov backward equations
- Nash equilibrium
- Price of anarchy