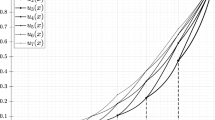
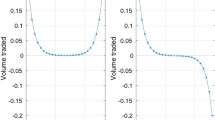
Abstract
We consider a deterministic model of market evolution with trading constraints and apply a game-theoretic approach to the superhedging problem. We obtain sufficient conditions for the game equilibrium and prove under these conditions the existence of a Borel-measurable transition kernel describing dependence on price prehistory of the most unfavourable mixed strategy of the market.
Similar content being viewed by others
Notes
The guaranteed deterministic approach was developed by us in the late 1990s (although at that period we were not aware of Kolokoltsov’s paper), but published (primarily in Russian) only in the last 5 years, together with some recent new results.
The dot “\(\,\cdot \,\)” indicates the variables representing the price evolution. More precisely, it indicates the prehistory \( {\bar{x}}_{t-1}=(x_0,\cdots , x_{t-1})\in (\mathbb {R}^n)^t \) for \( K_t \), and it indicates the history \( {\bar{x}}_t=(x_0,\cdots , x_{t})\in (\mathbb {R}^n)^{t+1} \) for the functions \( v^*_t \) and \( g_t \) introduced below.
The payoff function \(g_t\) is assumed to be bounded on the set of possible trajectories \(B_t\), \(t=1, \cdots , N\).
The neighbourhoods of points \(-\infty \) and \(+\infty \) are given by \([\infty , a)\), \(a \in \mathbb {R}\) and \((b, +\infty ]\), \(b \in \mathbb {R}\), respectively.
European or Bermudian options can be also considered using (1): if no payment is due at a moment of time t, we formally set \(g_t\equiv -\infty \).
Two notions of arbitrage introduced below, DAO (deterministic arbitrage opportunity) relates to “One Point Arbitrage” and in our setting is also equivalent to quasi-sure arbitrage of Bouchard and Nutz [3], while DSA (deterministic sure arbitrage) relates to “Strong Arbitrage”, to use the unified terminology of robust modelling in Burzoni, Frittelli, Hou, Maggis, and Obłój [7]. A detailed analysis of the relation between different “no arbitrage” notions in the framework for robust modelling of financial markets in discrete time is presented in Obłój and Wiesel [11].
Which is not the case for the traditional model with the reference probability, where the universe containing all states of the world is fixed (up to a set of zero measure) by means of considering equivalent measures. However, if all the absolute continuous measures with respect to a reference measure are considered (as in robust modelling), the uncertainty principle become applicable.
In order to avoid trivial cases, it is natural to consider the unbounded trading constraints \(D_t(\cdot ) \).
We feel now that the term “robust” is overused in the literature (with different meanings) and the term “coarse” would be better, but unfortunately “robust” is already used in our papers.
In fact, it can be weaken as follows: the convex hull of \({\tilde{K}}_t(x)\) need to be close to the convex hull of \(K_t(x) \), i.e. \(d_{\text {PH}}({{\,\textrm{conv}\,}}({\tilde{K}}_t(x)),{{\,\textrm{conv}\,}}( K_t(x) ))\leqslant \epsilon _t(x)\). Note that \(d_{\text {PHC}} (A,B) = d_{\text {PH}}({{\,\textrm{conv}\,}}(A),{{\,\textrm{conv}\,}}( B ))\leqslant d_{\text {PH}}(A, B )\) for compact sets A and B and \(d_{\text {PHC}}\) is a semimetric on the space of all compact set, being metric on the subspace of all compact convex sets.
In the probabilistic setting, this geometric criterion (understood almost surely) was found by Jacod and Shiryaev [14].
Note that in general RNDSAUP does not imply \({{\,\textrm{int}\,}}({{\,\textrm{conv}\,}}(K_t(\cdot ))) \ne \varnothing \).
For compact-valued mappings, h-continuity is equivalent to continuity; see, e.g. the book of Hu and Papageorgiou [17, Chapter 1, Theorem 2.68]
Note that in this case RNDSAUP is equivalent to RNDAO.
Under quite general assumptions, GDA pricing is not less the probabilistic pricing (almost surely) if consistency condition holds and there are simple examples where it is strictly greater.
Note that Proposition 3.8 in [21] is nevertheless valid, since the condition RNDAO is fulfilled for the one-dimensional case, i.e. for a single risky asset model.
Our example is reproduced in Carassus, Obłój and Wiesel [22]. Note that an additional assumption is added in this paper to obtain the correct sufficient conditions of superhedging price continuity; the corresponding result follows from our Theorem 1 by introducing artificial trading constraints \(D_t(\cdot )={{\,\textrm{span}\,}}(K_t(\cdot ) \), where \({{\,\textrm{span}\,}}(A) \) stands for the linear envelope of a set A. Moreover, in such a way the estimates of modulus of continuity become available.
The domain \(\mathcal {A}\) of Q, i. e., the \(\sigma \)-algebra of all subsets of \(\mathbb {R}^n\), can be chosen depending on a particular class \(\mathcal {P}_t(\cdot )\). For example, we can take as \(\mathcal {A}\) the class of all subsets if \(\mathcal {P}_t(\cdot )\) consists of probability measures concentrated in a finite set of points. In other cases, we can take, for example, a Borel \(\sigma \)-algebra, which is natural when the functions \(v^*_t\) are upper semicontinuous.
Hedger’s mixed strategies make no sense because the bracketed expression in (1) is a linear function of h (due to no transaction costs), and the set \(D_t(\cdot )\) is convex.
Note that the following inequality always holds: \(\rho _t(\cdot ) \geqslant \rho '_t(\cdot )\).
For example, as \(\mathcal {P}_t(\cdot )\) we can choose the class \(\mathcal {P}^*(K_t(\cdot ))\) of measures concentrated in a finite set of points from \(K_t(\cdot )\) (to avoid additional requirements on the functions \(v^*_t\)). An alternative approach involves, e.g. the universal measurability of \(v^*_t\) (or any other smoothness property, e.g. semicontinuity).
Here, \(\mathbb {R}\) is equipped with the Borel \(\sigma \)-algebra \(\mathcal {B}_{\mathbb {R}}\).
In the book [23], the term “stochastic kernel” was used.
Recall that \(K_t(\cdot )\ne \varnothing \) and \(D_t(\cdot )\ne \varnothing \) because \(0\in D_t(\cdot ).\)
That is, lower semicontinuous and closed.
The class \(\mathcal {P}^n(X)\) consists of all probability measures concentrated at most at \(n+1\) points of a space X; note that is not convex if X contains more than \(n+1\) points.
We follow the terminology of [17, Chapter 2, Definition 1.1]; note that there is a typo in item (a) of this definition. A set-valued mapping \(F(\cdot )\) is said to be strongly measurable with respect to a given \(\sigma \)-algebra \(\mathcal {F} \) (in our case, a Borel algebra) if \(F^-(C)=\{\omega \in \Omega :\;F(\omega )\cap C\ne \varnothing \}\in \mathcal {F}\) for any closed set \(C\subseteq Y\) and measurable if \(F^-(U)=\{\omega \in \omega :\; F(\omega )\cap U\ne \varnothing \}\in \mathcal {F}\) for any open set \(U\subseteq Y\). Immediately, if \(F(\cdot )\) is strongly measurable or measurable, then \({{\,\textrm{dom}\,}}F = \{\omega \in \omega :\; F(\omega )\ne \varnothing \}\in \mathcal {F}.\) Without loss of generality, such mappings \(F(\cdot )\) are assumed to have non-empty values.
Recall that we operate the weakest topology for which the functions \(Q\mapsto \int fdQ\) are continuous for any bounded continuous numerical function g on Y. (For a compact space Y, continuous numerical functions are always bounded.)
Moreover, it is compact, being a closed subset of a compact.
A compact set is closed in any enveloping Hausdorff space, particularly a metrizable one, such as the space of probability measures on Y with a Borel \(\sigma \)-algebra.
That is, a probability measure on \((Y,\mathcal {A})\), where the \(\sigma \)-algebra \(\mathcal {A}\) contains all singletons Y and the functions \(y\mapsto f(x,y)\) must be measurable with respect to \(\mathcal {A}\). In fact, a particular choice of \(\mathcal {A}\) is not needed for the first part of the theorem: it does not employ assumption 5. In this part, we can suppose that, e.g. \(\mathcal {A}\) is the \(\sigma \)-algebra of all at most countable subsets of Y. Then, the measurability condition is satisfied for any functions, and we consider only discrete distributions.
In other words, for any \(p=(p_1,\cdots ,p_n)\in S_{n-1}\), \(n\geqslant 1,\) and arbitrary \(y_i\in Y\), \(i=1,\cdots ,n,\) the functions \(x\mapsto \sum _{i=1}^n p_i f(x,y_i)\) are quasiconvex. In particular, the functions \(x\mapsto f(x,y)\), \(y\in Y,\) are quasiconvex.
Recall that \(D_t(\cdot )\) take convex values and \(0\in D_t(\cdot )\).
The set of feasible paths \(B_t\) is defined by the relation (1.2.1).
Here, we omit the fixed time instant and price history.
References
Smirnov, S.N.: A Guaranteed deterministic approach to superhedging: financial market model, trading constraints, and the Bellman-Isaacs equations. Autom. Remote Control. 82, 722–743 (2021)
Föllmer, H., Schied, A.: Stochastic finance. An introduction in discrete time, 4th edn. Walter de Gruyter, New York (2016)
Bouchard, B., Nutz, M.: Arbitrage and duality in nondominated discrete-time models. Ann. Appl. Probab. 25, 823–859 (2015)
Kolokoltsov, V.N.: Nonexpansive maps and option pricing theory. Kybernetika. 34, 713–724 (1998)
Bernhard, P., Engwerda, J.C., Roorda, B., Schumacher, J., Kolokoltsov, V., Saint-Pierre, P., Aubin, J.-P.: The Interval Market Model in Mathematical Finance: Game-Theoretic Methods. Springer, New York (2013)
Matsuda, T., Takemura, A.: Game-theoretic derivation of upper hedging prices of multivariate contingent claims and submodularity. Jpn. J. Indus Trial Appl. Math. 37, 213–248 (2020)
Burzoni, M., Frittelli, M., Hou, Z., Maggis, M., Obłój, J.: Pointwise arbitrage pricing theory in discrete time. Math. Op. Res. 44, 1034–1057 (2019)
Carassus, L., Vargiolu, T.: Super-replication price it can be ok. ESAIM Proc. Surv. 64, 54–64 (2018)
Smirnov, S.N.: A Guaranteed deterministic approach to superhedging: a game equilibrium in the case of no trading constraints. J. Math. Sci. 248, 105–115 (2020)
Carassus, L., Lépinette, E.: Pricing without no-arbitrage condition in discrete time. J. Math. Anal. Appl. 505, 125441 (2022)
Obłój, J., Wiesel, J.: A unified framework for robust modelling of financial markets in discrete time. Finance Stoch. 25, 427–468 (2021)
Smirnov, S.N.: A guaranteed deterministic approach to superhedging: no arbitrage properties of the market. Autom. Remote Control. 82, 172–187 (2021)
Smirnov, S.N.: Geometric criterion for a robust condition of no sure arbitrage with unlimited profit. Moscow Univ. Comput. Math. Cybern. 44, 146–150 (2020)
Jacod, J., Shiryaev, A.N.: Local martingales and the fundamental asset pricing theorems in the discrete-time case. Financ. Stochastics. 2, 259–273 (1998)
Smirnov, S.N.: Structural stability threshold for the condition of robust no deterministic sure arbitrage with unbounded profit. Moscow Univ. Comput. Math. Cybern. 45, 34–44 (2021)
Smirnov, S.N.: A guaranteed deterministic approach to the superhedging: semicontinuity and continuity properties of solutions of the Bellman-Isaacs equations. Autom. Remote Control. 82, 2024–2040 (2021)
Hu, S., Papageorgiou, N.: Handbook of Multivalued Analysis: Theory, Mathematics and Its Applications, vol. I. Springer, Berlin (1997)
Smirnov, S.N.: Guaranteed deterministic approach to superhedging: Lipschitz properties of solutions of the Bellman–Isaacs equations. In: Petrosyan, L., Mazalov, V., Zenkevich, N. (eds.) Frontiers of dynamic games. Static and dynamic game theory: Foundations and Applications. Birkhäuser Cham (2019) https://doi.org/10.1007/978-3-030-23699-1_14
Smirnov, S.N.: A guaranteed deterministic approach to superhedging: sensitivity of solutions of Bellman-Isaacs equations and numerical methods. Comput. Math. Model. 31, 384–401 (2020)
Smirnov, S.N.: A guaranteed deterministic approach to superhedging: the relationship between the deterministic and stochastic problem statement without trading constraints. Theory Probab. Appl. 67, 548–569 (2023)
Carassus, L., Obłój, J., Wiesel, J.: The robust superreplication problem: a dynamic approach. SIAM J. Financ. Math. 10, 907–941 (2019)
Carassus, L., Obłój, J., Wiesel, J.: Erratum to The robust superreplication problem: a dynamic approach. SIAM J. Financ. Math. 13, 653–655 (2022)
Bertsekas, D.P., Shreve, S.E.: Stochastic Optimal Control: The Discrete-Time Case. Academic Press, New York (1978)
Smirnov, S.N.: A guaranteed deterministic approach to superhedging optimal mixed strategies of the market and their supports. In: Karapetyants, A.N., Pavlov, I.V., Shiryaev, A.N. (eds.) Operator Theory and Harmonic Analysis. Springer, Cham (2021)
Lange, K.L.: Borel sets of probability measures. Pacific J. Math. 48, 141–162 (1973)
Smirnov, S.N.: General theorem on a finite support of mixed strategy in the theory of zero-sum games. Doklady Math. 97, 215–218 (2018)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflict of interest.
Additional information
This work was was supported by Moscow Center of Fundamental and Applied Mathematics (No.75-15-2022-284).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Smirnov, S.N. A Note on Transition Kernels for the Most Unfavourable Mixed Strategies of the Market. J. Oper. Res. Soc. China 12, 35–50 (2024). https://doi.org/10.1007/s40305-023-00490-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40305-023-00490-4
Keywords
- Superhedging
- Guaranteed deterministic approach
- Optimal mixed strategies of the market
- Borel-measurable transition kernel
- Game equilibrium