The Effect of Retailer’ Social Responsibility and Government Subsidy on the Performance of Low-Carbon Supply Chain

Abstract

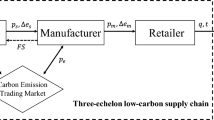
Based on the cap-and-trade regulation, the effect of retailer’s social responsibility and subsidy are analyzed in a two-level low-carbon supply chain. The government subsidizes manufacturer to encourage low-carbon technological innovation. It is gotten that both retailer’s social responsibility and subsidy can improve the profit of manufacturer and reduce the carbon emission level. Although more subsidies to manufacturer indeed may decrease the profit of retailer, it is good measure to promote the centralized decision-making between the retailer and manufacturer. A certain retailer’s social responsibilities are good for the carbon emission reduction, but it also brings about the decline of profit in the supply chain. The centralized decision-making is always the best choice strategy for the carbon emission reduction, while in the decentralized decision-making situation, the retailer has more possibilities to care about social responsibility.

Appendices

Appendix A

Proof of Theorem 1.

At the second stage, the retailer sets the retrial price to maximize its profit function, then

$$\mathop {{\text{max}}}\limits_{p} \;\pi_{{\text{R}}} {(}p;e,w{)} = \left( {p - w} \right)\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right).$$

(A1)

By Eq. (A1), $\frac{{\partial \pi_{{\text{R}}} }}{\partial p} = a - \gamma \left( {e_{0} - e} \right) + \beta w - 2\beta p$, let it equal zero, the solution is $p^{ * } = {a \mathord{\left/ {\vphantom {a {2\beta }}} \right. \kern-0pt} {2\beta }} + {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0pt} 2} - {{\gamma \left( {e_{0} - e} \right)} \mathord{\left/ {\vphantom {{\gamma \left( {e_{0} - e} \right)} {2\beta }}} \right. \kern-0pt} {2\beta }}$, while $\frac{{\partial^{2} \pi_{{\text{R}}} }}{{\partial p^{2} }} = - 2\beta < 0$. At the second stage, the manufacturer sets carbon emission and the wholesale price for their products to maximize its utility function, then

$$\mathop {\max }\limits_{e,w} \;\pi_{{\text{M}}} {(}e{,}w{)} = \left( {w - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right) - {{\lambda e^{2} } \mathord{\left/ {\vphantom {{\lambda e^{2} } 2}} \right. \kern-0pt} 2} + Kp_{e} .$$

Pugging $p^{ * }$ into manufacturer’s profit function $\pi_{{\text{M}}}$, we get that

$$\mathop {{\text{max}}}\limits_{e,w} \;\pi_{{\text{M}}} {(}e{,}w{)} = {{\left( {w - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - \beta w - \gamma \left( {e_{0} - e} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {w - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - \beta w - \gamma \left( {e_{0} - e} \right)} \right)} 2}} \right. \kern-0pt} 2} - {{\lambda e^{2} } \mathord{\left/ {\vphantom {{\lambda e^{2} } 2}} \right. \kern-0pt} 2} + Kp_{e} .$$

(A2)

Let the Hessian matrix of profit function be denoted by $H_{{\pi_{{\text{M}}} }}$. Primary sub formula of first order sequence ${\text{Det}}(H_{{\pi_{{\text{M}}} ,1}} ) = - \lambda { + }\gamma p_{e}$, and the primary sub formula of second order sequence ${\text{Det}}(H_{{\pi_{{\text{M}}} ,2}} ) = \beta \left( {\lambda - \gamma p_{e} } \right) - {{\left( {\gamma - p_{e} \beta } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\gamma - p_{e} \beta } \right)^{2} } 4}} \right. \kern-0pt} 4}$. When ${{\lambda \geqslant \left( {\gamma - p_{e} \beta } \right)^{2} } \mathord{\left/ {\vphantom {{\lambda \geqslant \left( {\gamma - p_{e} \beta } \right)^{2} } {4\beta }}} \right. \kern-0pt} {4\beta }}{ + }\gamma p_{e} = {{\left( {\gamma { + }p_{e} \beta } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\gamma { + }p_{e} \beta } \right)^{2} } {4\beta }}} \right. \kern-0pt} {4\beta }}$, ${\text{Det}}(H_{{\pi_{{\text{M}}} ,2}} ) \geqslant 0$ and ${\text{Det}}(H_{{\pi_{{\text{M}}} ,1}} ) = - \lambda { + }\gamma p_{e} \leqslant 0$. Therefore, $H_{{\pi_{{\text{M}}} }}$ is negative definite. The first-order conditions are

$$\left\{ \begin{gathered} \frac{{\partial \pi_{{\text{M}}} }}{\partial w} = \frac{{a - w\beta - \gamma \left( {e_{0} - e} \right)}}{2} - \frac{{\left( {w - \left( {e_{0} - e} \right)p_{e} } \right)\beta }}{2} = 0, \hfill \\ \frac{{\partial \pi_{{\text{M}}} }}{\partial e} = \frac{{p_{e} \left( {a - w\beta - \gamma \left( {e_{0} - e} \right)} \right)}}{2} + \frac{{\gamma \left( {w - \left( {e_{0} - e} \right)p_{e} } \right)}}{2} - \lambda e = 0. \hfill \\ \end{gathered} \right.$$

So

$$\begin{aligned} e^{ * } & = \frac{{\left( {\gamma + p_{e} \beta } \right)\left( {a - \left( {\gamma + p_{e} \beta } \right)e_{0} } \right)}}{{4\lambda \beta - \left( {\gamma { + }p_{e} \beta } \right)^{2} }} = \frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{\Delta }, \\ w^{ * } & = \frac{{\left( {2\lambda - p_{e} (\gamma + p_{e} \beta )} \right)a - 2\lambda (\gamma - p_{e} \beta )e_{0} }}{{4\lambda \beta - \left( {\gamma { + }p_{e} \beta } \right)^{2} }} = \frac{{\left( {2\lambda - p_{e} \eta_{1} } \right)a - 2\lambda \eta_{2} e_{0} }}{\Delta }, \\ p^{ * } & = \frac{a}{2\beta } + \frac{w}{2} - \frac{{\gamma \left( {e_{0} - e} \right)}}{2\beta } = \frac{{\left( {3\lambda - p_{e} \left( {p_{e} \beta { + }\gamma } \right)} \right)a{ + }\lambda \left( {p_{e} \beta - 3\gamma } \right)e_{0} }}{{4\beta \lambda - \left( {\gamma + p_{e} \beta } \right)^{2} }} \\ & = \frac{{\left( {3\lambda - p_{e} \eta_{1} } \right)a - \lambda \left( {2\eta_{1} { + }\eta_{2} } \right)e_{0} }}{\Delta }, \\ \end{aligned}$$

where $\Delta { = 4}\lambda \beta - \left( {\gamma { + }p_{e} \beta } \right)^{2}$, $\eta_{1} = \gamma { + }p_{e} \beta$ and $\eta_{2} = \gamma - p_{e} \beta$.

Proof of Proposition 1

By Eq. (3), there are

$$\frac{{\partial e^{ * } }}{\partial \lambda } = - \frac{{4\eta_{1} \beta \left( {a - \eta_{1} e_{0} } \right)}}{{\Delta^{2} }} \leqslant 0.$$

By Eq. (5), it is gotten that

$$\frac{{\partial p^{ * } }}{\partial \lambda } = \frac{{e_{{0}} \eta_{{1}}^{2} { + }a\eta_{{1}} \left( {3\beta p_{e} - \gamma } \right)}}{{{\Delta }^{2} }},$$

so $p_{e} \geqslant$ ${\gamma \mathord{\left/ {\vphantom {\gamma {3\beta }}} \right. \kern-0pt} {3\beta }}$, $\frac{{\partial p^{ * } }}{\partial \lambda } \geqslant$ 0.

Proof of Proposition 2

Without subsidy and customer surplus, the demand is

$$\begin{aligned} D^{*} & = a - \beta p^{*} - \gamma \left( {e_{0} - e^{*} } \right) = a - \beta \left( {\frac{a}{2\beta } + \frac{{w^{*} }}{2} - \frac{{\gamma \left( {e_{0} - e^{*} } \right)}}{2\beta }} \right) - \gamma \left( {e_{0} - e^{*} } \right) \\ & = \frac{{\left( {a - \beta w^{*} - \gamma \left( {e_{0} - e^{*} } \right)} \right)}}{2} = \frac{{\beta \lambda \left( {a - \eta_{1} e_{0} } \right)}}{\Delta }. \\ \end{aligned}$$

(A3)

Also, the profits of retailer and manufacturer are

$$\pi_{{\text{R}}}^{*} = \left( {p^{*} - w^{*} } \right)D^{*} = \left( {p^{*} - w^{*} } \right)\frac{{\beta \lambda \left( {a - \eta_{1} e_{0} } \right)}}{\Delta } = \frac{{\beta \lambda^{2} \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{\Delta^{2} }},$$

(A4)

$$\begin{aligned} \pi_{{\text{M}}}^{*} & = \left( {w^{*} - \left( {e_{0} - e^{*} } \right)p_{e} } \right)D^{*} - \frac{{\lambda e^{*2} }}{2} + Kp_{e} \\ & = \frac{{2\lambda^{2} \beta \left( {a - \left( {\gamma + p_{e} \beta } \right)e_{0} } \right)\left( {a - \left( {\gamma + p_{e} \beta } \right)e_{0} } \right)}}{{\Delta^{2} }} \\ &\quad - \frac{{\lambda \left( {\gamma + p_{e} \beta } \right)^{2} \left( {a - \left( {\gamma + p_{e} \beta } \right)e_{0} } \right)^{2} }}{{2\Delta^{2} }} + Kp_{e} \\ & = \frac{{\lambda \left( {a - \eta_{1} e_{0} } \right)^{2} }}{2\Delta } + Kp_{e} . \\ \end{aligned}$$

(A5)

Furthermore, the whole profit of SC is

$$\begin{aligned} \pi_{{\text{S}}}^{*} & = \pi_{{\text{M}}}^{*} + \pi_{{\text{R}}}^{*} = \frac{{\beta \lambda^{2} \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{\Delta^{2} }}{ + }\frac{{\lambda \left( {a - \eta_{1} e_{0} } \right)^{2} }}{2\Delta } + Kp_{e} \\ & = \frac{{\lambda \left( {2\beta \lambda { + }\Delta } \right)\left( {a - e_{0} \eta_{1} } \right)^{2} }}{{2\Delta^{2} }} + Kp_{e} . \\ \end{aligned}$$

(A6)

By Eqs. (A3), (A4), (A5) and (A6), we have that

$$\begin{aligned} \frac{{\partial D^{ * } }}{\partial \lambda } & = - \frac{{4\beta^{2} \left( {a - \eta_{1} e_{0} } \right)}}{{\Delta^{2} }} - \frac{{\left( {a - \eta_{1} e_{0} } \right)}}{\Delta } \leqslant 0, \\ \frac{{\partial \pi_{{\text{R}}}^{*} }}{\partial \lambda } & = - \frac{{8\beta^{2} \lambda^{2} \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{\Delta^{3} }} - \frac{{2\beta \lambda \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{\Delta^{2} }} \leqslant 0, \\ \frac{{\partial \pi_{{\text{M}}}^{*} }}{\partial \lambda } & = - \frac{{4\lambda \beta \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{2\Delta^{2} }} - \frac{{\left( {a - \eta_{1} e_{0} } \right)^{2} }}{2\Delta } \leqslant 0. \\ \end{aligned}$$

Furthermore, as $\pi_{{\text{S}}}^{*} = \pi_{{\text{M}}}^{*} + \pi_{{\text{R}}}^{*}$, we get that

$$\frac{{\partial \pi_{{\text{S}}}^{*} }}{\partial \lambda } \leqslant 0.$$

Proof of Theorem 2

When the cooperation is structured in the SC, the retailer and manufacturer set the carbon emission and price together to maximize the profit of SC, so

$$\mathop {{\text{max}}}\limits_{e,p} \;\pi_{{\text{s}}} = {{\left( {p - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {p - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right)} 2}} \right. \kern-0pt} 2} - {{\lambda e^{2} } \mathord{\left/ {\vphantom {{\lambda e^{2} } 2}} \right. \kern-0pt} 2} + Kp_{e}$$

(A7)

Let the Hessian matrix of profit function be denoted by $H_{{\pi_{{\text{s}}} }}$. Primary sub formula of first order sequence ${\text{Det}}(H_{{\pi_{{\text{S}}} ,1}} ) = - \lambda { + 2}\gamma p_{e}$, and the primary sub formula of second order sequence ${\text{Det}}(H_{{\pi_{{\text{S}}} ,2}} ) = 2\beta \lambda - \left( {\gamma + p_{e} \beta } \right)^{2}$. When ${{\lambda \geqslant \left( {\gamma { + }p_{e} \beta } \right)^{2} } \mathord{\left/ {\vphantom {{\lambda \geqslant \left( {\gamma { + }p_{e} \beta } \right)^{2} } {2\beta }}} \right. \kern-0pt} {2\beta }}$, ${\text{Det}}(H_{{\pi_{{\text{S}}} ,2}} ) \geqslant 0$ and ${\text{Det}}(H_{{\pi_{{\text{S}}} ,1}} ) = - \lambda { + 2}\gamma p_{e} \leqslant 0$. Therefore, $H_{{\pi_{{\text{S}}} }}$ is negative definite. The first-order conditions are

$$\left\{ \begin{gathered} \frac{{\partial \pi_{{\text{S}}} }}{\partial p} = a - 2\beta p - (\gamma - \beta p_{e} )\left( {e_{0} - e} \right) = 0, \hfill \\ \frac{{\partial \pi_{{\text{S}}} }}{\partial e} = p_{e} a + (\gamma - \beta p_{e} )p - 2\gamma p_{e} \left( {e_{0} - e} \right) - \lambda e = 0. \hfill \\ \end{gathered} \right.$$

So

$$\begin{aligned} e^{{**}} & = \frac{{\left( {\gamma + p_{e} \beta } \right)\left( {a - \left( {\gamma + p_{e} \beta } \right)e_{0} } \right)}}{{2\lambda \beta - \left( {\gamma { + }p_{e} \beta } \right)^{2} }} = \frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{\Delta - 2\lambda \beta }, \\ p^{{**}} & = \frac{a}{2\beta } - \frac{{\left( {\gamma - p_{e} \beta } \right)\left( {e_{0} - e} \right)}}{2\beta } = \frac{a}{2\beta } - \frac{{\left( {\gamma - p_{e} \beta } \right)\left( { - \eta_{1} a + 2\lambda \beta e_{0} } \right)}}{{2\beta \left( {\Delta - 2\beta \lambda } \right)}} \\ &= \frac{{\left( {\lambda \beta - p_{e} \beta \eta_{1} } \right)a - \lambda \eta_{2} e_{0} }}{{\beta \left( {\Delta - 2\beta \lambda } \right)}}, \\ \end{aligned}$$

where $\Delta { = 4}\lambda \beta - \left( {\gamma { + }p_{e} \beta } \right)^{2}$, $\eta_{1} = \gamma { + }p_{e} \beta$ and $\eta_{2} = \gamma - p_{e} \beta$.

Proof of Proposition 3

Comparing Theorem 1 and 2, we get $e^{{**}} \geqslant$ $e^{*}$ directly. Moreover, under the condition of centralized decision-making, the market demand is

$$D^{{**}} = a - \beta p^{{**}} - \gamma \left( {e_{0} - e^{{**}} } \right) = \frac{{\left( {a - \eta_{1} \left( {e_{0} - e^{*} } \right)} \right)}}{2} = \frac{{\beta \lambda \left( {a - \eta_{1} e_{0} } \right)}}{\Delta - 2\beta \lambda }.$$

Then we have that $D^{{**}} \geqslant D^{*}$. Furthermore, it is seen that

$$\begin{aligned} \pi_{{\text{S}}}^{{**}} &= \left( {p - \left( {e_{0} - e} \right)p_{e} } \right)D^{{**}} - \frac{{\lambda e^{**2} }}{2} + Kp_{e} = \frac{{\left( {a - \eta_{1} \left( {e_{0} - e^{**} } \right)} \right)}}{\beta }D^{{**}} - \frac{{\lambda e^{**2} }}{2} + Kp_{e} \quad \hfill \\ \quad \; &= \frac{{D^{{**2}} }}{\beta } - \frac{{\lambda e^{**2} }}{2} + Kp_{e} = \frac{{\beta \lambda^{2} \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{\left( {\Delta - 2\beta \lambda } \right)^{2} }} - \frac{{\lambda \eta_{1}^{2} \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{2\left( {\Delta - 2\beta \lambda } \right)^{2} }} + Kp_{e} \hfill \\ \quad \; &= \frac{{\lambda \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{2\left( {\Delta - 2\beta \lambda } \right)}} + Kp_{e} . \hfill \\ \end{aligned}$$

So by Eq. (A6), we have that

$$\pi_{{\text{S}}}^{**} - \pi_{{\text{S}}}^{*} = \frac{{\lambda \left( {a - e_{0} \eta_{1} } \right)^{2} }}{2}\left( {\frac{1}{\Delta - 2\beta \lambda } - \frac{{4\beta \lambda { + }\Delta }}{{\Delta^{2} }}} \right) = \frac{{\beta \lambda^{2} \eta_{1}^{2} \left( {a - e_{0} \eta_{1} } \right)^{2} }}{{\left( {\Delta - 2\beta \lambda } \right)\Delta^{2} }} \geqslant 0.$$

Therefore, we obtain that $\pi_{{\text{S}}}^{**} \geqslant \pi_{{\text{S}}}^{*}$.

Appendix B

Proof of Theorem 3

At the second stage, the retailer sets the retrial price to maximize its utility function, then

$$\mathop {{\text{max}}}\limits_{p} \;v_{{\text{R}}} = \left( {p - w} \right)\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right) + u\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right)^{2} /2.$$

(B1)

By Eq. (B1), $\frac{{\partial v_{{\text{R}}} }}{\partial p} = \left( {1 - \beta u} \right)a - \left( {1 - \beta u} \right)\gamma \left( {e_{0} - e} \right) + \beta w - \beta \left( {2 - \beta u} \right)p$, let it be equal zero, the solution is

$$p^{c * } = \frac{1 - \beta u}{{\beta \left( {2 - \beta u} \right)}}a + \frac{w}{2 - \beta u} - \frac{{\left( {1 - \beta u} \right)\gamma \left( {e_{0} - e} \right)}}{{\beta \left( {2 - \beta u} \right)}},$$

while $\frac{{\partial^{2} v_{{\text{R}}} }}{{\partial p^{2} }} = - 2\beta { + }u\beta < 0$. At the first stage, the manufacturer sets the carbon emission reduction level and the wholesale price to maximize its utility function, then

$$\mathop {{\text{max}}}\limits_{e,w} \;\pi_{{\text{M}}} = \left( {w - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right) - {{\lambda e^{2} } \mathord{\left/ {\vphantom {{\lambda e^{2} } 2}} \right. \kern-0pt} 2} + Kp_{e} .$$

Pugging $p^{c * }$ into manufacturer’s profit function $\pi_{M}$:

$$\;\pi_{{\text{M}}} = {{\left( {w - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - w\beta - \gamma \left( {e_{0} - e} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {w - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - w\beta - \gamma \left( {e_{0} - e} \right)} \right)} {\left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\left( {2 - \beta u} \right)}} - {{\lambda e^{2} } \mathord{\left/ {\vphantom {{\lambda e^{2} } 2}} \right. \kern-0pt} 2} + Kp_{e} .$$

(B2)

Let the Hessian matrix of profit function be denoted by $H_{{\pi_{{\text{M}}} }}$. Primary sub formula of first order sequence ${\text{Det}}(H_{{{\pi_{{\text{M}}} }}_{,1}} ) = - \lambda + {{2\gamma p_{e} } \mathord{\left/ {\vphantom {{2\gamma p_{e} } {\left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\left( {2 - \beta u} \right)}}$, and the primary sub formula of second order sequence ${\text{Det}}(H_{{\pi_{{\text{M}}} ,2}} ) = {{2\beta } \mathord{\left/ {\vphantom {{2\beta } {\left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\left( {2 - \beta u} \right)}}\left( {\lambda - {{2\gamma p_{e} } \mathord{\left/ {\vphantom {{2\gamma p_{e} } {\left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\left( {2 - \beta u} \right)}}} \right) - {{\left( {\gamma - p_{e} \beta } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\gamma - p_{e} \beta } \right)^{2} } {\left( {2 - \beta u} \right)^{2} }}} \right. \kern-0pt} {\left( {2 - \beta u} \right)^{2} }}$. When ${{\lambda \geqslant \left( {\gamma - p_{e} \beta } \right)^{2} } \mathord{\left/ {\vphantom {{\lambda \geqslant \left( {\gamma - p_{e} \beta } \right)^{2} } {2\beta \left( {2 - \beta u} \right)}}} \right. \kern-0pt} {2\beta \left( {2 - \beta u} \right)}}{ + }{{2\gamma p_{e} } \mathord{\left/ {\vphantom {{2\gamma p_{e} } {\left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\left( {2 - \beta u} \right)}} = {{\left( {\gamma { + }p_{e} \beta } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\gamma { + }p_{e} \beta } \right)^{2} } {2\beta \left( {2 - \beta u} \right)}}} \right. \kern-0pt} {2\beta \left( {2 - \beta u} \right)}}$ and $u \leqslant \min \left\{ {1,\;{2 \mathord{\left/ {\vphantom {2 {\beta ,\;{2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0pt} \beta } - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } {4\beta \lambda }}} \right. \kern-0pt} {4\beta \lambda }}}}} \right. \kern-0pt} {\beta ,\;{2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0pt} \beta } - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } {4\beta \lambda }}} \right. \kern-0pt} {4\beta \lambda }}}}} \right\}$, ${\text{Det}}(H_{{\pi_{{\text{M}}} ,2}} ) \geqslant 0$  and ${\text{Det}}(H_{{\pi_{{\text{M}}} ,1}} ) \leqslant 0$. Therefore, $H_{{\pi_{{\text{M}}} }}$ is negative definite. The first-order conditions are

$$\left\{ \begin{gathered} \frac{{\partial \pi_{{\text{M}}} }}{\partial w} = \frac{{a - w\beta - \gamma \left( {e_{0} - e} \right)}}{2 - \beta u} - \frac{{\left( {w - \left( {e_{0} - e} \right)p_{e} } \right)\beta }}{2 - \beta u} = 0, \hfill \\ \frac{{\partial \pi_{{\text{M}}} }}{\partial e} = \frac{{p_{e} \left( {a - w\beta - \gamma \left( {e_{0} - e} \right)} \right)}}{2 - \beta u} + \frac{{\gamma \left( {w - \left( {e_{0} - e} \right)p_{e} } \right)}}{2 - \beta u} - \lambda e = 0. \hfill \\ \end{gathered} \right.$$

So we have that

$$\begin{aligned} e^{c * } & = \frac{{\left( {\gamma + p_{e} \beta } \right)\left( {a - \left( {\gamma + p_{e} \beta } \right)e_{0} } \right)}}{{2\beta \lambda \left( {2 - \beta u} \right) - \left( {\gamma + p_{e} \beta } \right)^{2} }} = \frac{{\left( {\gamma + p_{e} \beta } \right)\left( {a - \left( {\gamma + p_{e} \beta } \right)e_{0} } \right)}}{{\Delta^{c} }}, \\ w^{c * } & = \frac{{\left( {\left( {2 - \beta u} \right)\lambda - p_{e} (\gamma + p_{c} \beta )} \right)a - \left( {2 - \beta u} \right)\lambda (\gamma - p_{e} \beta )e_{0} }}{{2\beta \lambda \left( {2 - \beta u} \right) - \left( {\gamma + p_{e} \beta } \right)^{2} }} \\ & = \frac{{\left( {\left( {2 - \beta u} \right)\lambda - p_{e} \eta_{1} } \right)a - \left( {2 - \beta u} \right)\lambda \eta_{2} e_{0} }}{{\Delta^{c} }}, \\ \end{aligned}$$

$$\begin{gathered} p^{c * } = \frac{{\left( {1 - \beta u} \right)a}}{{\beta \left( {2 - \beta u} \right)}} + \frac{{w^{c * } }}{2 - \beta u} - \frac{{\gamma \left( {1 - \beta u} \right)\left( {e_{0} - e^{c * } } \right)}}{{\beta \left( {2 - \beta u} \right)}} \hfill \\ \quad = \frac{{\left( {\left( {3 - 2\beta u} \right)\lambda - \eta_{1} p_{e} } \right)a - \lambda \left( {\left( {2 - \beta u} \right)\eta_{1} { + }\left( {1 - \beta u} \right)\eta_{2} } \right)e_{0} }}{{\Delta^{c} }},\quad \hfill \\ \end{gathered}$$

where $\Delta^{c} = 2\beta \lambda \left( {2 - \beta u} \right) - \left( {\gamma + p_{e} \beta } \right)^{2}$.

Proof of Proposition 4

Compared Theorem 1 and 3, it is seen that $e^{c*} \geqslant$ $e^{*}$, $w^{c*} \geqslant$ $w^{*}$ and $p^{c*} \geqslant$ $p^{*}$. With retailer’s CSR, the market demand is

$$D^{c * } = a - \beta p^{c * } - \gamma \left( {e_{0} - e^{c * } } \right)\, = \frac{{a\Delta^{c} - \eta_{1} \left( {2\left( {2 - \beta u} \right)\beta \lambda e_{0} - \eta_{1} a} \right)}}{{2\left( {2 - \beta u} \right)\Delta^{c} }}\, = \frac{{\beta \lambda \left( {a - \eta_{1} e_{0} } \right)}}{{\Delta^{c} }},$$

where $\Delta^{c} = 2\beta \lambda \left( {2 - \beta u} \right) - \left( {\gamma + p_{e} \beta } \right)^{2}$. By Eq. (6), the market demand without retailer’s CSR is $D^{*} = {{\beta \lambda \left( {a - \eta_{1} e_{0} } \right)} \mathord{\left/ {\vphantom {{\beta \lambda \left( {a - \eta_{1} e_{0} } \right)} \Delta }} \right. \kern-0pt} \Delta },$ where $\Delta { = 4}\lambda \beta - \left( {\gamma { + }p_{e} \beta } \right)^{2}$. It is gotten that $\Delta^{c} \leqslant$ $\Delta$, so $D^{c*} \geqslant$ $D^{*}$. With retailer’s CSR, the profit of manufacturer is obtained,

$$\begin{aligned} \pi_{{\text{M}}}^{c*} = &\left( {w^{c * } - \left( {e_{0} - e^{c * } } \right)p_{e} } \right)D^{*} - \frac{{\lambda e^{c *2} }}{2} + Kp_{e} \\ = &\frac{{\lambda \left( {a - \eta_{1} e_{0} } \right)^{2} \left[ {2\left( {2 - \beta u} \right)\beta \lambda - \eta_{1}^{2} } \right]}}{{2\left( {\Delta^{c} } \right)^{2} }} + Kp_{e} = \frac{{\lambda \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{2\Delta^{c} }} + Kp_{e} .\end{aligned}$$

Without Retailer’s CSR, by Eqs. (A4) and (A5), the profit of manufacturer is

$$\pi_{{\text{M}}}^{*} = \frac{{\lambda \left( {a - \eta_{1} e_{0} } \right)^{2} }}{2\Delta } + Kp_{e} .$$

It is not hard to get that $\pi_{{\text{M}}}^{c*} \geqslant$ $\pi_{{\text{M}}}^{*}$ when $u \leqslant \min \left\{ {1,\;{2 \mathord{\left/ {\vphantom {2 {\beta ,\;{2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0pt} \beta } - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } {4\beta^{{2}} \lambda }}} \right. \kern-0pt} {4\beta^{{2}} \lambda }}}}} \right. \kern-0pt} {\beta ,\;{2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0pt} \beta } - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } {4\beta^{{2}} \lambda }}} \right. \kern-0pt} {4\beta^{{2}} \lambda }}}}} \right\}$.

Proof of Theorem 4

When a cooperation is structured in the SC, the retailer and manufacturer set the carbon emission level and retail price to maximize the utility of SC, then

$$\begin{aligned} \mathop {{\text{max}}}\limits_{e,p} \;v_{{\text{S}}} = &\left( {p - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right) \\ &+ {{u\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right)^{2} } \mathord{\left/ {\vphantom {{u\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right)^{2} } 2}} \right. \kern-0pt} 2} - {{\lambda e^{2} } \mathord{\left/ {\vphantom {{\lambda e^{2} } 2}} \right. \kern-0pt} 2} + Kp_{e} .\end{aligned}$$

(B3)

Let the Hessian matrix of profit function be denoted by $H_{{v_{{\text{s}}} }}$. Primary sub formula of first order sequence ${\text{Det}}(H_{{v_{{\text{S}}} ,1}} ) = - \lambda { + 2}\gamma p_{e} { + }\gamma u$, and the primary sub formula of second order sequence is

${\text{Det}}(H_{{\pi_{{\text{M}}} ,2}} ) = \frac{2\beta }{{2 - \beta u}}\left( {\lambda - \frac{{2\gamma p_{e} { + }\gamma u}}{2 - \beta u}} \right) - \frac{{\left( {\gamma - p_{e} \beta - \beta u\gamma } \right)^{2} }}{{\left( {2 - \beta u} \right)^{2} }}$.

Because $u \leqslant \min \left\{ {1,\;{2 \mathord{\left/ {\vphantom {2 {\beta ,\;{2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0pt} \beta } - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } {4\beta \lambda }}} \right. \kern-0pt} {4\beta \lambda }}}}} \right. \kern-0pt} {\beta ,\;{2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0pt} \beta } - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } {4\beta \lambda }}} \right. \kern-0pt} {4\beta \lambda }}}}} \right\}$, it is gotten that ${{\lambda \geqslant \left( {\gamma + p_{e} \beta } \right)^{2} } \mathord{\left/ {\vphantom {{\lambda \geqslant \left( {\gamma + p_{e} \beta } \right)^{2} } {2\beta \left( {2 - \beta u} \right)}}} \right. \kern-0pt} {2\beta \left( {2 - \beta u} \right)}}$ and $u \leqslant \min \left\{ {1,\;{2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0pt} \beta }} \right\}$. Thus, we get ${\text{Det}}(H_{{v_{{\text{S}}} ,2}} ) \geqslant 0$ and ${\text{Det}}(H_{{v_{S} ,1}} ) \leqslant 0$. Therefore, $H_{{v_{{\text{S}}} }}$ is negative definite. The first-order conditions are

$$\left\{ \begin{gathered} \frac{{\partial \pi_{{\text{S}}} }}{\partial p} = \left( {1 - \beta u} \right)a - \beta \left( {2 - \beta u} \right)p - \left( {\left( {1 - \beta u} \right)\gamma - \beta p_{e} } \right)\left( {e_{0} - e} \right) = 0, \hfill \\ \frac{{\partial \pi_{{\text{S}}} }}{\partial e} = \left( {p_{e} + \gamma u} \right)a + \left( {\gamma - \beta \left( {p_{e} + \gamma u} \right)} \right)p - \gamma \left( {2p_{e} + \gamma u} \right)\left( {e_{0} - e} \right) - \lambda e = 0. \hfill \\ \end{gathered} \right.$$

So we have that

$$\begin{aligned} e^{c**} & = \frac{{\left( {\beta \left( {p_{e} + \gamma u} \right) + \left( {1 - \beta u} \right)\gamma } \right)\left( {a - \left( {\gamma { + }p_{e} \beta } \right)e_{0} } \right)}}{{\lambda \beta \left( {2 - \beta u} \right) - \left( {\beta \left( {p_{e} + \gamma u} \right) + \left( {1 - \beta u} \right)\gamma } \right)\left( {\gamma { + }p_{e} \beta } \right)}}\\ & = \frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{{\lambda \beta \left( {2 - \beta u} \right) - \eta_{1}^{2} }} = \frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{{\Delta^{c} - \lambda \beta \left( {2 - \beta u} \right)}}, \\ p^{c**} & = \frac{{\left( {1 - \beta u} \right)a - \left( {\left( {1 - \beta u} \right)\gamma - p_{e} \beta } \right)\left( {e_{0} - e} \right)}}{{\beta \left( {2 - \beta u} \right)}}\\ & = \frac{{\left( {\lambda \left( {2 - \beta u} \right) - \eta_{1} \left( {u\gamma + 2p_{e} } \right)} \right)a - \left( {\left( {1 - \beta u} \right)\gamma - p_{e} \beta } \right)\lambda \left( {2 - \beta u} \right)e_{0} }}{{\left( {2 - \beta u} \right)\left( {\Delta^{c} - \lambda \beta \left( {2 - \beta u} \right)} \right)}}{,} \\ \end{aligned}$$

where $\eta_{1} = \gamma { + }p_{e} \beta$ and $\eta_{2} = \gamma - p_{e} \beta$.

Proof of Proposition 5

By Eqs. (7) and (17),

$$\begin{aligned} e^{{**}} = &\frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{\Delta - 2\lambda \beta } = \frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{{2\lambda \beta - \left( {\gamma { + }p_{e} \beta } \right)^{2} }},\\ e^{c**} = & \frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{{\Delta^{c} - \lambda \beta \left( {2 - \beta u} \right)}} = \frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{{\beta \lambda \left( {2 - \beta u} \right) - \left( {\gamma + p_{e} \beta } \right)^{2} }}.\end{aligned}$$

It is not hard to get that $e^{c**} \geqslant$ $e^{**}$ when $u \leqslant \min \left\{ {1,\;{2 \mathord{\left/ {\vphantom {2 {\beta ,\;{2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0pt} \beta } - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } {4\beta \lambda }}} \right. \kern-0pt} {4\beta \lambda }}}}} \right. \kern-0pt} {\beta ,\;{2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0pt} \beta } - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } {4\beta \lambda }}} \right. \kern-0pt} {4\beta \lambda }}}}} \right\}$. Also, by Eqs. (3) and (17), we have that

$$\begin{aligned} e^{ * } =& \frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{{{4}\lambda \beta - \left( {\gamma { + }p_{e} \beta } \right)^{2} }},\\ e^{c * } =& \frac{{\left( {\gamma + p_{e} \beta } \right)\left( {a - \left( {\gamma + p_{e} \beta } \right)e_{0} } \right)}}{{\Delta^{c} }} = \frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{{2\beta \lambda \left( {2 - \beta u} \right) - \left( {\gamma + p_{e} \beta } \right)^{2} }}.\end{aligned}$$

Therefore, it is obtained that $e^{**} \geqslant$ $e^{c*} \geqslant$ $e^{*}$ because that $2 - \beta u \geqslant$ 1. Similarly, it is proved that $D^{c**} \geqslant$ $D^{**} \geqslant$ $D^{c*} \geqslant$ $D^{*}$.

Proof of Proposition 6

By Proposition 4, it is not hard to have that $\pi_{{\text{S}}}^{{**}} \geqslant$ $\pi_{{\text{S}}}^{*}$, since $\pi_{{\text{R}}}^{c*} \geqslant$ $\pi_{{\text{R}}}^{*}$ and $\pi_{{\text{M}}}^{c*} \geqslant$ $\pi_{{\text{M}}}^{*}$. Meanwhile, considering the CSR, the total profit of SC in the decentralized decision making situation is

$$\begin{aligned} \pi_{{\text{S}}}^{c*} & = \pi_{{\text{M}}}^{c*} + \pi_{{\text{R}}}^{c*} = \frac{{\left( {1 - \beta u} \right)\beta \lambda^{2} \left( {a - e_{0} \left( {\gamma + p_{e} \beta } \right)} \right)^{2} }}{{\left( {\Delta^{c} } \right)^{2} }}\\ &\quad + \frac{{\lambda \left( {a - \eta_{1} e_{0} } \right)^{2} \left[ {2\left( {2 - \beta u} \right)\beta \lambda - \eta_{1}^{2} } \right]}}{{2\left( {\Delta^{c} } \right)^{2} }} + Kp_{e} \\ & = \frac{{\lambda \left( {2\beta \left( {1 - \beta u} \right)\lambda { + }\Delta^{c} } \right)\left( {a - e_{0} \eta_{1} } \right)^{2} }}{{2\left( {\Delta^{c} } \right)^{2} }} + Kp_{e} . \\ \end{aligned}$$

Thus, we have that

$$\begin{aligned} \pi_{S}^{c**} - \pi_{S}^{c*} & = \frac{{\lambda \left( {a - e_{0} \eta_{1} } \right)^{2} }}{2}\left( {\frac{{\left( {\Delta^{c} - 2\beta \lambda } \right)}}{{\left( {\Delta^{c} - \left( {2 - \beta u} \right)\beta \lambda } \right)^{2} }} - \frac{{2\beta \left( {1 - \beta u} \right)\lambda + \Delta^{c} }}{{\left( {\Delta^{c} } \right)^{2} }}} \right) \\ & = \frac{{\lambda \left( {a - e_{0} \eta_{1} } \right)^{2} }}{2}\\ &\quad\left( {\frac{1}{{\Delta^{c} - \left( {2 - \beta u} \right)\beta \lambda }} - \frac{{\beta^{2} u\lambda }}{{\left( {\Delta^{c} - \left( {2 - \beta u} \right)\beta \lambda } \right)^{2} }} - \frac{{2\beta \left( {1 - \beta u} \right)\lambda + \Delta^{c} }}{{\left( {\Delta^{c} } \right)^{2} }}} \right) \\ & = \frac{{\lambda^{2} \beta^{2} \left( {a - e_{0} \eta_{1} } \right)^{2} }}{2}\\ &\quad\left( {\frac{u}{{\left( {\Delta - \left( {2 - \beta u} \right)\beta \lambda } \right)\Delta^{c} }} - \frac{u}{{\left( {\Delta^{c} - \left( {2 - \beta u} \right)\beta \lambda } \right)^{2} }} + \frac{{2\left( {2 - \beta u} \right)\left( {1 - \beta u} \right)}}{{\left( {\Delta^{c} - \left( {2 - \beta u} \right)\beta \lambda } \right)\Delta^{c} }}} \right) \\ & = \frac{{\lambda^{2} \left( {a - e_{0} \eta_{1} } \right)^{2} \beta^{2} }}{{2\left( {\Delta^{c} - \left( {2 - \beta u} \right)\beta \lambda } \right)}}\\ &\quad\left( {\frac{u}{{\Delta^{c} }} - \frac{u}{{\Delta^{c} - \left( {2 - \beta u} \right)\beta \lambda }} + \frac{{2\left( {2 - \beta u} \right)\left( {1 - \beta u} \right)}}{{\Delta^{c} }}} \right) \\ & = \frac{{\lambda^{2} \left( {2 - \beta u} \right)\left( {2 - 3\beta u} \right)\left( {a - e_{0} \eta_{1} } \right)^{2} \beta^{2} }}{{2\left( {\Delta^{c} - \left( {2 - \beta u} \right)\beta \lambda } \right)^{2} }}. \\ \end{aligned}$$

As

$$\pi_{{\text{S}}}^{{c{**}}} - \pi_{{\text{S}}}^{c*} = \frac{{\lambda^{2} \left( {2 - \beta u} \right)\left( {2 - 3\beta u} \right)\left( {a - e_{0} \eta_{1} } \right)^{2} \beta^{2} }}{{2\left( {\Delta^{c} - \left( {2 - \beta u} \right)\beta \lambda } \right)^{2} }} \geqslant 0,$$

it is gotten the conclusion that $\pi_{{\text{S}}}^{{c{**}}} \geqslant$ $\pi_{{\text{S}}}^{c*}$.

Proof of Theorem 5

At the second stage, the retailer sets the retrial price to maximize its utility function, then

$$\mathop {{\text{max}}}\limits_{p} \;v_{{\text{R}}} = \left( {p - w} \right)\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right) + u\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right)^{2} /2.$$

(B4)

By Eq. (B4), $\frac{{\partial v_{{\text{R}}} }}{\partial p} = \left( {1 - \beta u} \right)a - \left( {1 - \beta u} \right)\gamma \left( {e_{0} - e} \right) + \beta w - \beta \left( {2 - \beta u} \right)p$, let it be equal zero, the solution is

$$p^{s * } = {{\left( {1 - \beta u} \right)a} \mathord{\left/ {\vphantom {{\left( {1 - \beta u} \right)a} {\beta \left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\beta \left( {2 - \beta u} \right)}} + {w \mathord{\left/ {\vphantom {w {\left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\left( {2 - \beta u} \right)}} - {{\left( {1 - \beta u} \right)\gamma \left( {e_{0} - e} \right)} \mathord{\left/ {\vphantom {{\left( {1 - \beta u} \right)\gamma \left( {e_{0} - e} \right)} {\beta \left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\beta \left( {2 - \beta u} \right)}},$$

while $\frac{{\partial^{2} v_{{\text{R}}} }}{{\partial p^{2} }} = - 2\beta { + }u\beta < 0$. At the first stage, the manufacturer sets carbon emission and the wholesale price for their products to maximize its utility function, then

$$\mathop {{\text{max}}}\limits_{e,w} \;\pi_{{\text{M}}} = \left( {w - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right) - {{\lambda e^{2} } \mathord{\left/ {\vphantom {{\lambda e^{2} } 2}} \right. \kern-0pt} 2} + Kp_{e}.$$

Pugging $p^{s * }$ into M’s profit function $\pi_{M}$:

$$\;\pi_{{\text{M}}} = {{\left( {w - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - w\beta - \gamma \left( {e_{0} - e} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {w - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - w\beta - \gamma \left( {e_{0} - e} \right)} \right)} {\left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\left( {2 - \beta u} \right)}} - {{\left( {\lambda - \theta } \right)e^{2} } \mathord{\left/ {\vphantom {{\left( {\lambda - \theta } \right)e^{2} } 2}} \right. \kern-0pt} 2} + Kp_{e} .$$

(B5)

Let the Hessian matrix of profit function be denoted by $H_{{\pi_{{\text{M}}} }}$. Primary sub formula of first order sequence ${\text{Det}}(H_{{{\pi_{{\text{M}}} }}_{,1}} ) = - \left( {\lambda - \theta } \right) + {{2\gamma p_{e} } \mathord{\left/ {\vphantom {{2\gamma p_{e} } {\left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\left( {2 - \beta u} \right)}}$, and the primary sub formula of second order sequence

$${\text{Det}}(H_{{\pi_{{\text{M}}} ,2}} ) = \frac{2\beta }{{2 - \beta u}}\left( {\left( {\lambda - \theta } \right) - \frac{{2\gamma p_{e} }}{2 - \beta u}} \right) - \frac{{\left( {\gamma - p_{e} \beta } \right)^{2} }}{{\left( {2 - \beta u} \right)^{2} }}.$$

When

$$\lambda \geqslant \frac{{\left( {\gamma - p_{e} \beta } \right)^{2} }}{{2\beta \left( {2 - \beta u} \right)}} + \frac{{2\gamma p_{e} }}{2 - \beta u} + \theta = \frac{{\left( {\gamma + p_{e} \beta } \right)^{2} }}{{2\beta \left( {2 - \beta u} \right)}} + \theta ,$$

${\text{Det}}(H_{{\pi_{{\text{M}}} ,2}} ) \geqslant 0$ and ${\text{Det}}(H_{{\pi_{{\text{M}}} ,1}} ) \leqslant 0$. Therefore, $H_{{\pi_{{\text{M}}} }}$ is negative definite. The first-order conditions are

$$\left\{ \begin{gathered} \frac{{\partial \pi_{{\text{M}}} }}{\partial w} = \frac{{a - w\beta - \gamma \left( {e_{0} - e} \right)}}{2 - \beta u} - \frac{{\left( {w - \left( {e_{0} - e} \right)p_{e} } \right)\beta }}{2 - \beta u} = 0, \hfill \\ \frac{{\partial \pi_{{\text{M}}} }}{\partial e} = \frac{{p_{e} \left( {a - w\beta - \gamma \left( {e_{0} - e} \right)} \right)}}{2 - \beta u} + \frac{{\gamma \left( {w - \left( {e_{0} - e} \right)p_{e} } \right)}}{2 - \beta u} - \left( {\lambda - \theta } \right)e = 0. \hfill \\ \end{gathered} \right.$$

So

$$\begin{aligned} e^{s * } & = \frac{{\left( {\gamma + p_{e} \beta } \right)\left( {a - \left( {\gamma + p_{e} \beta } \right)e_{0} } \right)}}{{2\beta \left( {\lambda - \theta } \right)\left( {2 - \beta u} \right) - \left( {\gamma + p_{e} \beta } \right)^{2} }} = \frac{{\left( {\gamma + p_{e} \beta } \right)\left( {a - \left( {\gamma + p_{e} \beta } \right)e_{0} } \right)}}{{\Delta^{s} }}, \\ w^{s * } & = \frac{{\left( {\left( {2 - \beta u} \right)\left( {\lambda - \theta } \right) - p_{e} (\gamma + p_{e} \beta )} \right)a - \left( {2 - \beta u} \right)\left( {\lambda - \theta } \right)(\gamma - p_{e} \beta )e_{0} }}{{2\beta \left( {\lambda - \theta } \right)\left( {2 - \beta u} \right) - \left( {\gamma + p_{e} \beta } \right)^{2} }} \\ & = \frac{{\left( {\left( {2 - \beta u} \right)\left( {\lambda - \theta } \right) - p_{e} \eta_{1} } \right)a - \left( {2 - \beta u} \right)\left( {\lambda - \theta } \right)\eta_{2} e_{0} }}{{\Delta^{s} }}, \\ p^{s * } & = \frac{{\left( {1 - \beta u} \right)a}}{{\beta \left( {2 - \beta u} \right)}} + \frac{{w^{s * } }}{2 - \beta u} - \frac{{\gamma \left( {1 - \beta \mu } \right)\left( {e_{0} - e^{s * } } \right)}}{{\beta \left( {2 - \beta u} \right)}} \\ & = \frac{{\left( {\left( {3 - 2\beta u} \right)\left( {\lambda - \theta } \right) - \eta_{1} p_{e} } \right)a - \left( {\lambda - \theta } \right)\left( {\left( {3 - 2\beta u} \right)\gamma - p_{e} \beta } \right)e_{0} }}{{\Delta^{s} }} \\ & = \frac{{\left( {\left( {3 - 2\beta u} \right)\left( {\lambda - \theta } \right) - \eta_{1} p_{e} } \right)a - \left( {\lambda - \theta } \right)\left( {\left( {2 - \beta u} \right)\eta_{1} { + }\left( {1 - \beta u} \right)\eta_{2} } \right)e_{0} }}{{\Delta^{s} }}.\end{aligned}$$

where $\Delta^{s} = 2\beta \left( {\lambda - \theta } \right)\left( {2 - \beta u} \right) - \left( {\gamma + p_{e} \beta } \right)^{2}$.

Proof of Lemma 1

As

$$\begin{aligned} \frac{\partial f}{{\partial {\varvec{x}}}} & = - \frac{{2\beta \left( {2 - \beta u} \right)}}{{x^{2} }} - \frac{{2\left( {\gamma + p_{e} \beta } \right)^{2} }}{{x^{3} }} ,\\ \frac{{\partial^{2} f}}{{\partial x^{2} }} & = \frac{{4\beta \left( {2 - \beta u} \right)}}{{x^{3} }} + \frac{{8\left( {\gamma + p_{e} \beta } \right)^{2} }}{{x^{4} }} \geqslant 0, \\ \end{aligned}$$

it is gotten that $f{(}x{)}$ is concave function. Hence, we do not repeat it here.

Proof of Theorem 6

With the subsidy, the market demand in the decentralized making decision situation $D^{s * }$ is

$$\begin{aligned} D^{s * } & = a - \beta p^{s*} - \gamma \left( {e_{0} - e^{s*} } \right) \\ & = a - \beta \left( {\frac{1 - \beta u}{{\beta \left( {2 - \beta u} \right)}}a + \frac{{w^{s * } }}{2 - \beta u} - \frac{{\left( {1 - \beta u} \right)\gamma \left( {e_{0} - e^{s*} } \right)}}{{\beta \left( {2 - \beta u} \right)}}} \right) - \gamma \left( {e_{0} - e^{s*} } \right) \\ & = \frac{a}{2 - \beta u} - \frac{{\beta w^{s * } }}{2 - \beta u} - \frac{{\gamma \left( {e_{0} - e^{s*} } \right)}}{2 - \beta u} = \frac{{a - \eta_{1} \left( {e_{0} - e^{s*} } \right)}}{{2\left( {2 - \beta u} \right)}} \\ & = \frac{{\Delta^{s} - \eta_{1} \left( {2\left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)e_{0} - \eta_{1} a} \right)}}{{2\left( {2 - \beta u} \right)\Delta^{s} }} \\ & = \frac{{\beta \left( {\lambda - \theta } \right)\left( {a - \eta_{1} e_{0} } \right)}}{{\Delta^{s} }}. \\ \end{aligned}$$

Thus, the profits and manufacturer and retailer are

$$\begin{aligned} \pi_{R}^{s * } & = \left( {p^{s* } - w^{s* } } \right)D^{s* } \\ & = \left( {\frac{a}{\beta } - w^{s* } - \frac{{\gamma \left( {e_{0} - e^{s* } } \right)}}{\beta }} \right)D^{{c}^{ * }} = \frac{{\left( {1 - \beta u} \right)\left( {D^{s * } } \right)^{2} }}{\beta } \\ & = \frac{{\left( {1 - \beta u} \right)\beta \left( {\lambda - \theta } \right)^{2} \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{\Delta^{s} }} \\ & = \frac{{\left( {1 - \beta u} \right)\beta \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{\frac{{2\beta \left( {2 - \beta u} \right)}}{\lambda - \theta } - \frac{{\left( {\gamma + p_{e} \beta } \right)^{2} }}{{\left( {\lambda - \theta } \right)^{2} }}}}. \\ \end{aligned}$$

$$\begin{aligned} \pi_{M}^{s*} & = \left( {w^{s * } - \left( {e_{0} - e^{s * } } \right)p_{c} } \right)D^{s*} - \frac{{\lambda e^{s * 2} }}{2} + Kp_{e} \\ & = \frac{{\left( {2 - \beta u} \right)\beta \lambda \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{\left( {\Delta^{s} } \right)^{2} }} - \frac{{\lambda \eta_{1}^{2} \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{2\left( {\Delta^{s} } \right)^{2} }} + Kp_{e} \\ & = \frac{{\left( {\lambda - \theta } \right)\left( {a - \eta_{1} e_{0} } \right)^{2} \left[ {2\left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right) - \eta_{1}^{2} } \right]}}{{2\left( {\Delta^{s} } \right)^{2} }} + Kp_{e} \\ & = \frac{{\left( {\lambda - \theta } \right)\left( {a - \eta_{1} e_{0} } \right)^{2} }}{{2\Delta^{s} }} + Kp_{e} . \\ \end{aligned}$$

By Lemma 1, if $\theta = \lambda - {{\left( {\gamma + p_{e} \beta } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\gamma + p_{e} \beta } \right)^{2} } {\beta \left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\beta \left( {2 - \beta u} \right)}}$, then $\pi_{{\text{R}}}^{s * }$ gets its minimum value, and

$$\frac{{\partial \pi_{{\text{M}}}^{s * } }}{\partial \lambda } = \frac{{\left( {a - \eta_{1} e_{0} } \right)^{2} \left[ {2\beta (2 - \beta u)\left( {\lambda - \theta } \right)) + \left( {\gamma + p_{e} \beta } \right)^{2} } \right]}}{{\left( {\Delta^{s} } \right)^{2} }} \geqslant 0.$$

Therefore, the conclusion is gotten.

Proof of Theorem 7

When a cooperation is structured in the SC, retailer and manufacturer set the carbon emission level and retail price to maximize the utility of SC, and

$$\pi_{{\text{S}}} = \pi_{{\text{M}}} + \pi_{{\text{R}}} = \left( {p - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right) - {{\left( {\lambda - \theta } \right)e^{2} } \mathord{\left/ {\vphantom {{\left( {\lambda - \theta } \right)e^{2} } 2}} \right. \kern-0pt} 2} + Kp_{e} ,$$

(B6)

$$\begin{aligned}\mathop {{\text{max}}}\limits_{e,p} v_{{\text{S}}} &= \pi_{{\text{S}}} + \mu CS = \left( {p - \left( {e_{0} - e} \right)p_{e} } \right)\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right)\\ &\quad + {{u\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right)^{2} } \mathord{\left/ {\vphantom {{u\left( {a - \beta p - \gamma \left( {e_{0} - e} \right)} \right)^{2} } 2}} \right. \kern-0pt} 2} - {{\left( {\lambda - \theta } \right)e^{2} } \mathord{\left/ {\vphantom {{\left( {\lambda - \theta } \right)e^{2} } 2}} \right. \kern-0pt} 2} + Kp_{e} . \end{aligned}$$

(B7)

Let the Hessian matrix of profit function be denoted by $H_{{v_{s} }}$. Primary sub formula of first order sequence ${\text{Det}}(H_{{v_{{\text{S}}} ,1}} ) = - \left( {\lambda - \theta } \right){ + 2}\gamma p_{e} { + }\gamma u$, and the primary sub formula of second order sequence ${\text{Det}}(H_{{v_{{\text{S}}} ,2}} ) = 2\beta \left( {\lambda - \theta } \right) - \left( {\gamma + p_{e} \beta } \right)^{2}$. When $\theta \leqslant \lambda - {{\left( {\gamma - p_{e} \beta + \gamma u} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\gamma - p_{e} \beta + \gamma u} \right)^{2} } {\beta \left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\beta \left( {2 - \beta u} \right)}} - \gamma \left( {u + 2p_{e} } \right)$ and $u \leqslant \min \left\{ {1,\;{2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0pt} \beta }} \right\}$, we get that ${\text{Det}}(H_{{v_{{\text{S}}} ,2}} ) \geqslant$ 0 and ${\text{Det}}(H_{{v_{{\text{S}}} ,1}} ) \leqslant 0$. Therefore, $H_{{v_{{\text{S}}} }}$ is negative definite. The first-order conditions are

$$\left\{ \begin{gathered} \frac{{\partial \pi_{{\text{S}}} }}{\partial p} = \left( {1 - \beta u} \right)a - \beta \left( {2 - \beta u} \right)p - \left( {\left( {1 - \beta u} \right)\gamma - \beta p_{e} } \right)\left( {e_{0} - e} \right) = 0, \hfill \\ \frac{{\partial \pi_{{\text{S}}} }}{\partial e} = \left( {p_{e} + \gamma u} \right)a + \left( {\gamma - \beta \left( {p_{e} + \gamma u} \right)} \right)p - \gamma \left( {2p_{e} + \gamma u} \right)\left( {e_{0} - e} \right) - \left( {\lambda - \theta } \right)e = 0. \hfill \\ \end{gathered} \right.$$

So

$$\begin{aligned} e^{s**} & = \frac{{\left( {\beta \left( {p_{e} + \gamma u} \right) + \left( {1 - \beta u} \right)\gamma } \right)\left( {a - \left( {\gamma + p_{e} \beta } \right)e_{0} } \right)}}{{\left( {\lambda - \theta } \right)\beta \left( {2 - \beta u} \right) - \left( {\beta \left( {p_{e} + \gamma u} \right) + \left( {1 - \beta u} \right)\gamma } \right)\left( {\gamma + p_{e} \beta } \right)}} \\ & = \frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{{\left( {\lambda - \theta } \right)\beta \left( {2 - \beta u} \right) - \eta_{1}^{2} }} = \frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{{\Delta^{s} - \left( {\lambda - \theta } \right)\beta \left( {2 - \beta u} \right)}}, \\ p^{s**} & = \frac{{\left( {1 - \beta u} \right)a - \left( {\left( {1 - \beta u} \right)\gamma - p_{e} \beta } \right)\left( {e_{0} - e^{s**} } \right)}}{{\beta \left( {2 - \beta u} \right)}} \\ & = \frac{{\left( {\left( {\lambda - \theta } \right)\left( {2 - \beta u} \right) - \eta_{1} \left( {u\gamma + 2p_{e} } \right)} \right)a - \left( {\left( {1 - \beta u} \right)\gamma - p_{e} \beta } \right)\left( {\lambda - \theta } \right)\left( {2 - \beta u} \right)e_{0} }}{{\left( {2 - \beta u} \right)\left( {\Delta^{s} - \left( {\lambda - \theta } \right)\beta \left( {2 - \beta u} \right)} \right)}}, \\ \end{aligned}$$

where $\eta_{1} = \gamma { + }p_{e} \beta$ and $\eta_{2} = \gamma - p_{e} \beta$.

Proof of Proposition 7

• (1) As the coefficient a is big enough, we have that

  $$\begin{aligned} \frac{{\partial e^{*} }}{\partial \gamma } & = \frac{{a\eta_{1}^{2} + 2\beta (a - 2e_{0} \eta_{1} ) \cdot 2\lambda }}{{\Delta^{2} }} \geqslant 0,\;\;\;\frac{{\partial e^{*} }}{{\partial p_{e} }} = \frac{{a\eta_{1}^{2} + 2\beta (a - 2e_{0} \eta_{1} ) \cdot 2\lambda }}{{\Delta^{2} }}\beta \geqslant 0 \\ \frac{{\partial e^{**} }}{\partial \gamma } & = \frac{{a\eta_{1}^{2} + \beta (a - 2e_{0} \eta_{1} ) \cdot 2\lambda }}{{(2\lambda \beta - \eta_{1}^{2} )^{2} }} \geqslant 0,\;\;\;\frac{{\partial e^{**} }}{{\partial p_{e} }} = \frac{{a\eta_{1}^{2} + \beta (a - 2e_{0} \eta_{1} ) \cdot 2\lambda }}{{\Delta^{2} }}\beta \geqslant 0. \\ \end{aligned}$$

• (2) As $u \leqslant \min \{ 1,{2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0pt} \beta }\}$, we get that

  $$\begin{aligned} \frac{{\partial e^{c*} }}{\partial \gamma } & = \frac{{a\eta_{1}^{2} + 2\beta (a - 2e_{0} \eta_{1} ) \cdot (2 - \beta u)\lambda }}{{(\Delta^{c} )^{2} }} \geqslant 0,\\ \frac{{\partial e^{c*} }}{{\partial p_{e} }} &= \frac{{a\eta_{1}^{2} + 2\beta (a - 2e_{0} \eta_{1} ) \cdot (2 - \beta u)\lambda }}{{(\Delta^{c} )^{2} }}\beta \geqslant 0, \\ \frac{{\partial e^{c**} }}{\partial \gamma } & = \frac{{a\eta_{1}^{2} + \beta (a - 2e_{0} \eta_{1} ) \cdot (2 - \beta u)\lambda }}{{(\lambda \beta (2 - \beta u) - \eta_{1}^{2} )^{2} }} \geqslant 0,\\ \frac{{\partial e^{c**} }}{{\partial p_{e} }}& = \frac{{a\eta_{1}^{2} + \beta (a - 2e_{0} \eta_{1} ) \cdot (2 - \beta u)\lambda }}{{(\lambda \beta (2 - \beta u) - \eta_{1}^{2} )^{2} }}\beta \geqslant 0. \\ \end{aligned}$$

• (3) Due to $u \leqslant \min \{ 1,{2 \mathord{\left/ {\vphantom {2 \beta }} \right. \kern-0pt} \beta }\}$ and $\theta \leqslant \lambda - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } {2\beta \left( {2 - \beta u} \right)}}} \right. \kern-0pt} {2\beta \left( {2 - \beta u} \right)}}$, we obtain that

  $$\begin{aligned} \frac{{\partial e^{s*} }}{\partial \gamma } & = \frac{{a\eta_{1}^{2} + 2\beta (a - 2e_{0} \eta_{1} ) \cdot (2 - \beta u)(\lambda - \theta )}}{{(\Delta^{s} )^{2} }} \geqslant 0, \\ \frac{{\partial e^{s*} }}{{\partial p_{e} }} & = \frac{{a\eta_{1}^{2} + 2\beta (a - 2e_{0} \eta_{1} ) \cdot (2 - \beta u)(\lambda - \theta )}}{{(\Delta^{s} )^{2} }}\beta \geqslant 0, \\ \frac{{\partial e^{s**} }}{\partial \gamma } & = \frac{{a\eta_{1}^{2} + \beta (a - 2e_{0} \eta_{1} ) \cdot (2 - \beta u)(\lambda - \theta )}}{{((\lambda - \theta )\beta (2 - \beta u) - \eta_{1}^{2} )^{2} }} \geqslant 0, \\ \frac{{\partial e^{s**} }}{{\partial p_{e} }} & = \frac{{a\eta_{1}^{2} + \beta (a - 2e_{0} \eta_{1} ) \cdot (2 - \beta u)(\lambda - \theta )}}{{((\lambda - \theta )\beta (2 - \beta u) - \eta_{1}^{2} )^{2} }}\beta \geqslant 0. \\ \end{aligned}$$

Proof of Theorem 8

With the subsidy, the whole profit of SC in the centralized decision-making situation is

$$\begin{aligned} \pi_{S}^{s**} & = \left( {p^{s**} - \left( {e_{0} - e} \right)p_{e} } \right)D^{s**} - \frac{{\left( {\lambda - \theta } \right)\left( {e^{s**} } \right)^{2} }}{2} + Kp_{e}\\ & = \frac{{\left( {1 - \beta u} \right)\left( {a - \eta_{1} \left( {e_{0} - e^{s**} } \right)} \right)}}{{\left( {2 - \beta u} \right)\beta }}D^{**} - \frac{{\left( {\lambda - \theta } \right)\left( {e^{s**} } \right)^{2} }}{2} + Kp_{e} \\ & = \frac{{\left( {1 - \beta u} \right)\left( {D^{s**} } \right)^{2} }}{\beta } - \frac{{\left( {\lambda - \theta } \right)\left( {e^{s**} } \right)^{2} }}{2} + Kp_{e} \\ &= \frac{{\left( {1 - \beta u} \right)\beta \left( {\lambda - \theta } \right)^{2} \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{\left( {\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)} \right)^{2} }} - \frac{{\left( {\lambda - \theta } \right)\eta_{1}^{2} \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{2\left( {\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)} \right)^{2} }} + Kp_{e} \\ & = \frac{{\left( {\lambda - \theta } \right)\left( {a - \eta_{1} e_{0} } \right)^{2} \left( {\Delta^{s} - 2\beta \left( {\lambda - \theta } \right)} \right)}}{{2\left( {\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)} \right)^{2} }} + Kp_{e} . \\ \end{aligned}$$

The utility of SC in the centralized decision-making situation is

$$\begin{aligned} v_{S}^{s**} & = \pi_{S}^{s**} + uCS\; = \frac{{\left( {\lambda - \theta } \right)\left( {a - \eta_{1} e_{0} } \right)^{2} \left( {\Delta^{s} - 2\beta \left( {\lambda - \theta } \right)} \right)}}{{2\left( {\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)} \right)^{2} }} + Kp_{e} + \frac{{\mu \left( {D^{c**} } \right)^{2} }}{2} \\ & = \frac{{\left( {\lambda - \theta } \right)\left( {a - \eta_{1} e_{0} } \right)^{2} \left( {\Delta^{s} - 2\beta \left( {\lambda - \theta } \right)} \right)}}{{2\left( {\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)} \right)^{2} }} + Kp_{e} + \frac{{\mu \beta^{2} \left( {\lambda - \theta } \right)^{2} \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{2\left( {\Delta^{s} - \left( {\lambda - \theta } \right)\beta \left( {2 - \beta u} \right)} \right)^{2} }} \\ & = \frac{{\left( {\lambda - \theta } \right)\left( {a - \eta_{1} e_{0} } \right)^{2} }}{{2\left( {\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)} \right)}} + Kp_{e} . \\ \end{aligned}$$

By Remark 2, there is

$$v_{{\text{S}}}^{c**} = \pi_{{\text{S}}}^{c**} + \mu CS\; = \frac{{\lambda \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{2\left( {\Delta^{c} - \left( {2 - \beta u} \right)\beta \lambda } \right)}} + Kp_{e},$$

so $v_{{\text{S}}}^{s**} \leqslant v_{{\text{S}}}^{c**}$. The profit of supply in decentralized decision-making situation is

$$\begin{aligned} \pi_{S}^{s*} & = \pi_{M}^{s*} + \pi_{R}^{s*} \\ & = \frac{{\left( {1 - \beta u} \right)\beta \left( {\lambda - \theta } \right)^{2} \left( {a - e_{0} \left( {\gamma + p_{e} \beta } \right)} \right)^{2} }}{{\left( {\Delta^{s} } \right)^{2} }}\\ & \quad + {\kern 1pt} \;\frac{{\lambda \left( {a - \eta_{1} e_{0} } \right)^{2} \left[ {2\left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right) - \eta_{1}^{2} } \right]}}{{2\left( {\Delta^{s} } \right)^{2} }} + Kp_{e} \\ & = \frac{{\left( {\lambda - \theta } \right)\left( {2\beta \left( {1 - \beta u} \right)\left( {\lambda - \theta } \right) + \Delta^{s} } \right)\left( {a - e_{0} \eta_{1} } \right)^{2} }}{{2\left( {\Delta^{s} } \right)^{2} }} + Kp_{e} . \\ \end{aligned}$$

Hence, it is obvious that $\pi_{{\text{S}}}^{s**} \geqslant \pi_{{\text{S}}}^{s*}$. Also, the utility of supply in decentralized decision-making situation is

$$\begin{aligned} v_{S}^{s*} & = \pi_{S}^{s*} + v_{R}^{s*} = \frac{{\left( {\lambda - \theta } \right)\left( {2\beta \left( {1 - \beta u} \right)\left( {\lambda - \theta } \right) + \Delta^{s} } \right)\left( {a - e_{0} \eta_{1} } \right)^{2} }}{{2\left( {\Delta^{s} } \right)^{2} }} + Kp_{e} + \frac{{u\left( {D^{s * } } \right)^{2} }}{2} \\ & = \frac{{\left( {\lambda - \theta } \right)\left( {2\beta \left( {1 - \beta u} \right)\left( {\lambda - \theta } \right) + \Delta^{c} } \right)\left( {a - e_{0} \eta_{1} } \right)^{2} }}{{2\left( {\Delta^{s} } \right)^{2} }} + Kp_{e} + \frac{{u\beta^{2} \left( {\lambda - \theta } \right)^{2} \left( {a - \eta_{1} e_{0} } \right)^{2} }}{{2\left( {\Delta^{s} } \right)^{2} }} \\ & = \frac{{\left( {\lambda - \theta } \right)\left( {\left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right) + \Delta^{c} } \right)\left( {a - e_{0} \eta_{1} } \right)^{2} }}{{2\left( {\Delta^{s} } \right)^{2} }} + Kp_{e} . \\ \end{aligned}$$

Thus, we have that

$$\begin{aligned} \pi_{S}^{s**} - \pi_{S}^{s*} & = \frac{{\left( {\lambda - \theta } \right)\left( {a - e_{0} \eta_{1} } \right)^{2} }}{2}\\ &\quad\left( \frac{{\Delta^{s} - 2\beta \left( {\lambda - \theta } \right)}}{{\left( {\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)} \right)^{2} }}- \frac{{2\beta \left( {1 - \beta u} \right)\left( {\lambda - \theta } \right) + \Delta^{s} }}{{\left( {\Delta^{s} } \right)^{2} }} \right) \\ & = \frac{{\left( {\lambda - \theta } \right)\left( {a - e_{0} \eta_{1} } \right)^{2} }}{2}\\ &\quad\left( \frac{1}{{\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)}} - \frac{{\beta^{2} u\left( {\lambda - \theta } \right)}}{{\left( {\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)} \right)^{2} }} \right.\\ &\quad\left.- \frac{{2\beta \left( {1 - \beta u} \right)\left( {\lambda - \theta } \right) + \Delta^{s} }}{{\left( {\Delta^{s} } \right)^{2} }} \right) \\ & = \frac{{\left( {\lambda - \theta } \right)^{2} \beta^{2} \left( {a - e_{0} \eta_{1} } \right)^{2} }}{2}\\ &\quad\left( \frac{u}{{\left( {\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)} \right)\Delta^{s} }} - \frac{u}{{\left( {\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)} \right)^{2} }}\right.\\ &\quad\left. + \frac{{2\left( {2 - \beta u} \right)\left( {1 - \beta u} \right)}}{{\left( {\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)} \right)\Delta^{s} }} \right) \\ & = \frac{{\left( {\lambda - \theta } \right)^{2} \left( {a - e_{0} \eta_{1} } \right)^{2} \beta^{2} }}{{2\left( {\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)} \right)}}\\ &\quad\left( {\frac{u}{{\Delta^{s} }} - \frac{u}{{\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)}} + \frac{\begin{gathered} 2\left( {2 - \beta u} \right)\left( {1 - \beta u} \right) \hfill \\ \end{gathered} }{{\Delta^{s} }}} \right) \\ & = \frac{{\left( {\lambda - \theta } \right)^{2} \left( {2 - \beta u} \right)\left( {2 - 3\beta u} \right)\left( {a - e_{0} \eta_{1} } \right)^{2} \beta^{2} }}{{2\left( {\Delta^{s} - \left( {2 - \beta u} \right)\beta \left( {\lambda - \theta } \right)} \right)^{2} }}. \\ \end{aligned}$$

It is gotten that $\pi_{{\text{S}}}^{s**} - \pi_{{\text{S}}}^{s*} \geqslant$ $\pi_{{\text{S}}}^{c**} - \pi_{{\text{S}}}^{c*}$. This proof is completed.

Proof of Theorem 9

The proof is similar to Theorem 6. When the subsidy is at a certain point $\theta = \lambda - {{\left( {\eta_{2} + \gamma u} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\eta_{2} + \gamma u} \right)^{2} } {\beta \left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\beta \left( {2 - \beta u} \right)}} - \gamma \left( {u + 2p_{e} } \right)$, the profit of the SC is the smallest. Because $\lambda - {{\left( {\eta_{2} + \gamma u} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\eta_{2} + \gamma u} \right)^{2} } {\beta \left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\beta \left( {2 - \beta u} \right)}} - \gamma \left( {u + 2p_{e} } \right) \leqslant \lambda - {{\left( {\eta_{2} + \gamma u} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\eta_{2} + \gamma u} \right)^{2} } {\beta \left( {2 - \beta u} \right)}}} \right. \kern-0pt} {\beta \left( {2 - \beta u} \right)}} - \gamma \left( {u + 2p_{e} } \right)$, so $\frac{{\partial \pi_{{\text{S}}}^{{s{*}*}} }}{\partial \theta } \leqslant 0$.

Proof of Theorem 10

We have gotten that

$$\begin{aligned} e^{c * } & = \frac{{\left( {\gamma + p_{e} \beta } \right)\left( {a - \left( {\gamma + p_{e} \beta } \right)e_{0} } \right)}}{{\Delta^{c} }},\;\;\;e^{c**} = \frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{{\Delta^{c} - \lambda \beta \left( {2 - \beta u} \right)}}, \\ e^{s * } & = \frac{{\left( {\gamma + p_{e} \beta } \right)\left( {a - \left( {\gamma + p_{e} \beta } \right)e_{0} } \right)}}{{\Delta^{s} }},\;\;\;e^{{s{**}}} = \frac{{\eta_{1} \left( {a - \eta_{1} e_{0} } \right)}}{{\Delta^{s} - \left( {\lambda - \theta } \right)\beta \left( {2 - \beta u} \right)}}. \\ \end{aligned}$$

Because $\Delta^{s} = 2\beta \left( {\lambda - \theta } \right)\left( {2 - \beta u} \right) - \left( {\gamma + p_{e} \beta } \right)^{2} \leqslant 2\beta \lambda \left( {2 - \beta u} \right) - \left( {\gamma + p_{e} \beta } \right)^{2} = \Delta^{c}$, so we also get that $e^{s**} \geqslant e^{c**}$ and $e^{s*} \geqslant e^{c*}$. By Proposition 5, we get that $D^{c**} \geqslant D^{**} \geqslant D^{c*}$. In a similar way, it is obtained that $D^{s**} \geqslant D^{s*} \geqslant D^{c*} \geqslant D^{*}$. Hence, we only need to prove that $D^{c**} \geqslant D^{s*}.$

$$\begin{aligned} D^{c**} - D^{s * } & = \frac{{\beta \lambda \left( {a - \eta_{1} e_{0} } \right)}}{{\Delta^{c} - \lambda \beta \left( {2 - \beta u} \right)}} - \frac{{\beta \left( {\lambda - \theta } \right)\left( {a - \eta_{1} e_{0} } \right)}}{{\Delta^{s} }} \\ & = \beta \left( {a - \eta_{1} e_{0} } \right)\left( {\frac{1}{{\beta \left( {2 - \beta u} \right) - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } \lambda }} \right. \kern-0pt} \lambda }}} - \frac{1}{{2\beta \left( {2 - \beta u} \right) - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } {\left( {\lambda - \theta } \right)}}} \right. \kern-0pt} {\left( {\lambda - \theta } \right)}}}}} \right). \\ \end{aligned}$$

Furthermore, we have that

$$\begin{aligned} & \left( {2\beta \left( {2 - \beta u} \right) - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } {\left( {\lambda - \theta } \right)}}} \right. \kern-0pt} {\left( {\lambda - \theta } \right)}}} \right) - \left( {\beta \left( {2 - \beta u} \right) - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } \lambda }} \right. \kern-0pt} \lambda }} \right)\\ &\quad = \beta \left( {2 - \beta u} \right) - {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } {\left( {\lambda - \theta } \right)}}} \right. \kern-0pt} {\left( {\lambda - \theta } \right)}} + {{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } \lambda }} \right. \kern-0pt} \lambda } \\ &\quad = \frac{{\beta \left( {2 - \beta u} \right)\left( {\lambda - \theta } \right)\lambda - \eta_{1}^{2} \lambda + \eta_{1}^{2} \left( {\lambda - \theta } \right)}}{{\left( {\lambda - \theta } \right)\lambda }} = \frac{{\beta \left( {2 - \beta u} \right)\left( {\lambda - \theta } \right)\lambda - \eta_{1}^{2} \theta }}{{\left( {\lambda - \theta } \right)\lambda }} \\ &\quad \geqslant \frac{{\left( {{{\eta_{1}^{2} } \mathord{\left/ {\vphantom {{\eta_{1}^{2} } {\beta \left( {2 - \beta u} \right){ + }\theta }}} \right. \kern-0pt} {\beta \left( {2 - \beta u} \right){ + }\theta }}} \right)\eta_{1}^{2} - \eta_{1}^{2} \theta }}{{\left( {\lambda - \theta } \right)\lambda }} \geqslant 0. \\ \end{aligned}$$

Thus, it is gotten that

$D^{{c{\text{**}}}} - D^{{s * }} = \beta \left( {a - \eta _{1} e_{0} } \right)\left( {\frac{1}{{\beta \left( {2 - \beta u} \right) - \eta _{1} ^{2} /\lambda }} - \frac{1}{{2\beta \left( {2 - \beta u} \right) - \eta _{1} ^{2} /\left( {\lambda - \theta } \right)}}} \right) \geqslant 0.$