Skip to main content

Advertisement

Springer Nature Link
Log in

Equilibrium Strategies in a Fluid Queue with Working Vacations

  • Published:
Journal of the Operations Research Society of China Aims and scope Submit manuscript

Abstract

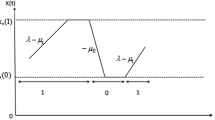
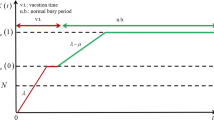
We consider a fluid queue with working vacations. Once the buffer becomes empty during the normal working period, the buffer will enter a working vacation period during which the outflow rate of fluids will be switched to a lower rate than that in normal working period. After this working vacation period, if the buffer is non-empty, the outflow rate of fluids will be switched to normal rate immediately; otherwise, the buffer will enter another working vacation until the buffer is non-empty after one working vacation. For such a fluid queue, based on the utility function, we analyze the strategic behavior of the fluids, regarding the joining/balking dilemma, under the fully observable case, almost observable case and fully unobservable case. Furthermore, the expected equilibrium social benefits under different cases are discussed. At last, the optimal social benefit strategy is analyzed and the inefficiency of the equilibrium strategies is quantified via the Price of Anarchy (PoA) measure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Mitra, D.: Stochastic theory of a fluid model of producers and consumers coupled by a buffer. Adv. Appl. Probab. 20, 646–676 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  2. Broek, M.A.J.U.H., Van, der. Heide. G., Van, Foreest. N. D.: Energy-saving policies for temperature-controlled production systems with state-dependent setup times and costs. Eur. J. Oper. Res. 287(3), 916-928 (2020)

  3. Nabli, H., Abbessi, W., Ouerghi, H.: A unified algorithm for finite and finite buffer content distribution of Markov fluid models. Perform. Eval. 99–100, 37–54 (2016)

    Google Scholar 

  4. Abbessi, W., Nabli, H.: General approach for video traffic: from modeling to optimization. Multimed. Syst. 25, 177–193 (2019)

    Article  Google Scholar 

  5. Bean, N.G., O’Reilly, M.M., Sargison, J.E.: A stochastic fluid flow model of the operation and maintenance of power generation systems. IEEE. Trans. Power. Syst. 25(3), 1361–1374 (2010)

    Article  Google Scholar 

  6. O’Reilly, M.M.: Multi-stage stochastic fluid models for congestion control. Eur. J. Oper. Res. 238, 514–526 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  7. Deiana, E., Latouche, G., Remiche, M.A.: Fluid flow model for energy-aware server performance evaluation. Methodol. Comput. Appl. Probab. 23, 801–821 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  8. Zychlinski, N.: Applications of fluid models in service operations management. Queueing. Syst. 103(1–2), 161–185 (2023)

    Article  MathSciNet  MATH  Google Scholar 

  9. Kosten, L.: Stochastic theory of multi-entry buffer, part 1. Delft Progress Re- port, Series F 1, 10–18 (1974)

  10. Kosten, L.: Stochastic theory of multi-entry buffer, part 2. Delft Progress Re- port, Series F 1, 44–55 (1974)

  11. Kosten, L., Vrieze, O.J.: Stochastic theory of multi-entry buffer, part 3. Delft Progress Report, Series F 1, 103–115 (1975)

  12. Anick, D., Mitra, D.: Stochastic theory of a data-handling system with multiple sources. Bell. Labs. Tech. J. (1982)

  13. Virtamo, J., Norros, I.: Fluid queue driven by an M/M/1 queue. Queueing. Syst. 16, 373–386 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  14. Parthasarathy, P.R., Vijayashree, K.V., Lenin, R.B.: An M/M/1 driven fluid queue-continued fraction approach. Queueing. Syst. 42, 189–199 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  15. Sericola, B., Parthasarathy, P.R., Vijayashree, K.V.: Exact transient solution of an M/M/1 driven fluid queue. Int. J. Comput. Math. 82(6), 659–671 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  16. Li, W., Liu, Y., Zhao, Y.Q.: Exact tail asymptotics for fluid models driven by an M/M/c queue. Queueing. Syst. 91, 319–346 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  17. Bean, N.G., O’Reilly, M.M.: Performance measures of a multi-layer Markovian fluid model. Ann. Oper. Res. 160, 99–120 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  18. He, Q.M., Wu, H.: Multi-layer MMFF processes and the MAP/PH/K+ GI queue: theory and algorithms. Queue. Models Serv. Manage. 3(1), 37–88 (2020)

    Google Scholar 

  19. Liu, Y., Whitt, W.: A network of time-varying many-server fluid queues with customer abandonment. Oper. Res. 59, 835–846 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  20. Hall, R.: Patient flow. AMC 10, 12 (2013)

    Google Scholar 

  21. Levy, Y., Yechiali, U.: Utilization of idle time in an M / G /1 queueing system. Manag. Sci. 22, 202–211 (1975)

    Article  MATH  Google Scholar 

  22. Takagi, H.: Queueing Analysis: A Foundation of Performance Evaluation. vol I: Vacation and Priority Systems. North-Holland (1991)

  23. Tian, N., Zhang, Z.G.: Vacation Queueing Models. Springer, Berlin (2006)

    Book  MATH  Google Scholar 

  24. Servi, L.D., Finn, S.G.: M/M/1 queues with working vacation (M/M/1/WV). Perform. Eval. 50, 41–52 (2002)

    Article  Google Scholar 

  25. Liu, W., Xu, X., Tian, N.: Stochastic decompositions in the M/M/1 queue with working vacations. Oper. Res. Lett. 35, 595–600 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  26. Wu, D., Takagi, H.: M/G/1 queue with multiple working vacations. Perform. Eval. 63, 654–681 (2006)

    Article  Google Scholar 

  27. Kim, J.D., Choi, D.W., Chae, K.C.: Analysis of queue-length distribution of the M/G/1 queue with Working Vacation. In: Hawaii international conference on statistics and related fields (2003)

  28. Li, J., Tian, N., Zhang, Z.G., Luh, H.P.: Analysis of the M/G/1 queue with exponentially working vacations-a matrix analytic approach. Queueing. Syst. 61, 139–166 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  29. Baba, Y.: Analysis of a GI/M/1 queue with multiple working vacations. Oper. Res. Lett. 33, 654–681 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  30. Li, J., Tian, N.: Performance analysis of an G/M/1 queue with single working vacation. Appl. Math. Comput. 217, 4960–4971 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  31. Chae, K., Lim, D., Yang, W.: The GI/M/1 queue and the GI/Geo/1 queue both with single working vacation. Perform. Eval. 66, 356–367 (2009)

    Article  Google Scholar 

  32. Li, T., Wang, Z., Liu, Z.: The GI/M/1 queue with Bernouli-schedule-controlled vacation and vacation interruption. Appl. Math. Model. 37, 3724–3735 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  33. Mao, B.W., Wang, F.W., Tian, N.S.: Fluid model driven by an M / M /1 queue with multiple vacations and N-policy. J. Appl. Math. Comput. 38, 119–131 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  34. Ammar, S.I.: Analysis of an M/M/1 driven fluid queue with multiple exponential vacations. Appl. Math. Comput. 227, 329–334 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  35. Xu, X., Wang, X., Song, X., Li, X.: Fluid model modulated by an M/M/1 working vacation queue with negative customer. Acta. Math. Appl. Sin-E. 34, 404–15 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  36. Vijayashree, K.V., Anjuka, A.: Stationary analysis of a fluid queue driven by an M/M/1/N queue with disaster and subsequent repair. Int. J. Oper. Res. 31, 461–77 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  37. Xu, X., Wang, H.: Analysis of fluid model modulated by an M/PH/1 working vacation queue. J. Syst. Sci. Syst. Eng. 28, 132–140 (2019)

    Article  Google Scholar 

  38. Naor, P.: The regulation of queue size by levying tolls. Econometrica 37, 15–24 (1969)

    Article  MATH  Google Scholar 

  39. Haviv, M., Ravner, L.: Strategic bidding in an accumulating priority queue: equilibrium analysis. Ann. Oper. Res. 244, 505–523 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  40. Bountali, O., Economou, A.: Strategic customer behavior in a two-stage batch processing system. Queueing. Syst. 93, 3–29 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  41. Dvir, N., Hassin, R., Yechiali, U.: Strategic behaviour in a tandem queue with alternating server. Queueing. Syst. 96, 205–244 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  42. Wang, J., Zhang, Y., Zhang, Z.G.: Strategic joining in an M/M/K queue with asynchronous and synchronous multiple vacations. J. Oper. Res. Soc. 72, 161–179 (2021)

    Article  Google Scholar 

  43. Yang, L., Wang, Z., Cui, S.: A model of queue scalping. Manag. Sci. 67, 6803–6821 (2021)

    Article  Google Scholar 

  44. Hassin, R.: Rational Queueing. CRC Press, Boca Raton (2016)

    MATH  Google Scholar 

  45. Economou, A., Manou, A.: Strategic behavior in an observable fluid queue with an alternating service process. Eur. J. Oper. Res. 254, 148–160 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  46. Logothetis, D., Manou, A., Economou, A.: The impact of reneging on a fluid on-off queue with strategic customers. Ann. Oper. Res. (2022). https://doi.org/10.1007/s10479-022-04807-z

    Article  MATH  Google Scholar 

  47. Servi, L.D., Finn, S.G.: M/M/1 queues with working vacation (M/M/1/WV). Perform. Eval. 50, 41–52 (2002)

    Article  Google Scholar 

  48. Muslu, K.; Bird, C.; Nagappan, N.; Czerwonka, J. Transition from centralized to decentralized version control systems: a case study on reasons, barriers, and outcomes. In: 36th International conference on software engineering (Icse 2014) , pp. 334-344 (2014)

  49. Lee, K., Shah, N.B., Huang, L.B., Ramchandran, K.: The MDS queue: analysing the latency performance of erasure codes. IEEE Trans. Inform Theory 63, 2822–2842 (2017)

    MathSciNet  MATH  Google Scholar 

  50. Koutsoupias, E., Papadimitriou, C.: Worst-case equilibria. Comput. Sci. Rev. 3, 65–69 (1999)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the anonymous referees for their constructive comments that help us to improve the present paper.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Nanjing University of Information Science and Technology, Nanjing, 210044, Jiangsu, China

    Si-Jia Cai, Qing-Qing Ye & Yu-Fei Liu

Authors
  1. Si-Jia Cai
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Qing-Qing Ye
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yu-Fei Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

S.-J. Cai contributed to the analysis and manuscript preparation; Q.-Q. Ye contributed to the conception of the study and helped perform the analysis with constructive discussions; Y.-F. Liu performed the experiment.

Corresponding author

Correspondence to Qing-Qing Ye.

Ethics declarations

Conflict of Interest

The authors declare that they have no competing interests

Additional information

The research was supported by the National Natural Science Foundation of China (Nos. 11901307 and 42275160).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cai, SJ., Ye, QQ. & Liu, YF. Equilibrium Strategies in a Fluid Queue with Working Vacations. J. Oper. Res. Soc. China (2023). https://doi.org/10.1007/s40305-023-00517-w

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40305-023-00517-w

Keywords

Mathematics Subject Classification